题目内容
在平面直角坐标系xOy中,已知点P(-3,3),点Q在x轴上,△PQO是等腰三角形,则满足条件的点Q共有( )
| A、5个 | B、4个 | C、3个 | D、2个 |
考点:等腰三角形的判定,坐标与图形性质
专题:
分析:分别以P、O为圆心,PO长为半径画圆,作线段PO与x轴的交点即满足条件,可得出答案.
解答: 解:
解:
∵P点坐标为(-3,3),
∴OP=3
,
如图,分别以P、O为圆心,PO长为半径画圆,分别交x轴于点A、B和C点,
再作PO的垂直平分线交x轴于点D,
所以满足条件的Q点共有四个,
故选B.
 解:
解:∵P点坐标为(-3,3),
∴OP=3
| 2 |
如图,分别以P、O为圆心,PO长为半径画圆,分别交x轴于点A、B和C点,
再作PO的垂直平分线交x轴于点D,
所以满足条件的Q点共有四个,
故选B.
点评:本题主要考查等腰三角的判定,利用圆上的点到圆心的距离都相等找到满足条件的点是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
根据下表的对应值,试判断一元二次方程ax2+bx+c=0的一解的取值范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.07 |
| A、3<x<3.23 |
| B、3.23<x<3.24 |
| C、3.24<x<3.25 |
| D、3.25<x<3.26 |
 已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.给出以下四个结论:①∠EBC=22.5°;②AE=2EC;③劣弧AE是劣弧DE的2倍;④DE=DC.其中不正确结论的序号是( )
已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.给出以下四个结论:①∠EBC=22.5°;②AE=2EC;③劣弧AE是劣弧DE的2倍;④DE=DC.其中不正确结论的序号是( )| A、① | B、④ | C、③ | D、② |
如果三个有理数的积是负数,那么这三个有理数中( )
| A、只有一个负数 |
| B、有两个负数 |
| C、三个都是负数 |
| D、有一个或三个负数 |
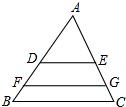 如图,△ABC中,BC=15,DE∥FG∥BC且将△ABC面积三等分,则DE+FG=
如图,△ABC中,BC=15,DE∥FG∥BC且将△ABC面积三等分,则DE+FG=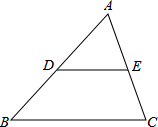 如图,在△ABC中,D、E分别为边AB、AC的中点.
如图,在△ABC中,D、E分别为边AB、AC的中点.