题目内容
4.(1)计算:(sin30°)-1-(2015)0+|1-$\sqrt{3}$|-$\sqrt{12}$.(2)解不等式组:$\left\{\begin{array}{l}{x+3>0}\\{2(x-1)+3≥3x}\end{array}\right.$,并判断x=$\sqrt{3}$是否为该不等式组的解.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用零指数幂法则计算,第三项利用绝对值的代数意义化简,最后一项化为最简二次根式,计算即可得到结果;
(2)分别求出不等式中两不等式的解集,找出解集的公共部分确定出不等式组的解集,即可做出判断.
解答 解:(1)原式=2-1+$\sqrt{3}$-1-2$\sqrt{3}$=-$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{x+3>0①}\\{2(x-1)+3≥3x②}\end{array}\right.$,
由①得:x>-3,
由②得:x≤1,
∴不等式组的解集为-3<x≤1,
则x=$\sqrt{3}$不是不等式组的解.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
6.某班30位女生所穿鞋子的尺码.数据如下(单位:码):
记众数为a,中位数为b,则a+b=70.
| 码号 | 33 | 34 | 35 | 36 | 37 |
| 人数 | 7 | 6 | 15 | 1 | 1 |
9.绵阳到某地相距n千米,提速前火车从绵阳到某地要t小时,提速后行车时间减少了0.5小时,提速后火车的速度比原来速度快了( )
| A. | $\frac{n}{t-0.5}$ | B. | $\frac{n}{t}$ | C. | $\frac{n}{t-0.5}$-$\frac{n}{t}$ | D. | $\frac{n}{t}$-$\frac{n}{t-0.5}$ |
16.当x取任意实数时,下列各根式有意义的是( )
| A. | $\sqrt{x+1}$ | B. | $\sqrt{\frac{x-1}{2}}$ | C. | $\sqrt{\frac{3}{{x}^{2}}}$ | D. | $\sqrt{|x|+1}$ |
13.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm、2cm、4cm | B. | 8cm、6cm、3cm | C. | 2cm、6cm、3cm | D. | 11cm、4cm、6cm |
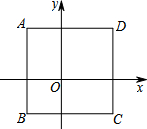 如图,正方形ABCD在平面直角坐标系中,其中三个顶点的坐标分别为A(-2,3),B(-2,-2),C(3,-2),则第四个顶点D的坐标为(3,3).
如图,正方形ABCD在平面直角坐标系中,其中三个顶点的坐标分别为A(-2,3),B(-2,-2),C(3,-2),则第四个顶点D的坐标为(3,3).
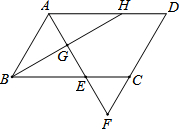 如图,?ABCD中,∠DAB的平分线交BC于E,交DC的延长线于F,∠ABC的平分线交AD于点H,交AF于点G.
如图,?ABCD中,∠DAB的平分线交BC于E,交DC的延长线于F,∠ABC的平分线交AD于点H,交AF于点G.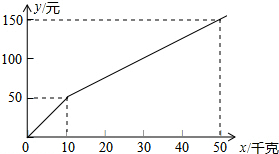 某种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格打折,因此付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如果所示,下列四种说法:
某种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格打折,因此付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如果所示,下列四种说法: