Question

5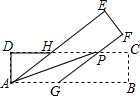．如图，在矩形ABCD中，点P在边CD上，连接AP，将矩形ABCD沿AP折叠，点B，点C的对应点分别是点E，点F，延长FP交边AB于点G，AE交边CD于点H．
（1）求证：四边形AGPH是菱形；
（2）若AB=4，BC=1，设AH=x，直接写出x的取值范围．

Answer 1

分析 （1）利用平行四边形的判定方法得出四边形AGPH是平行四边形，进而得出AH=PH，进而得出平行四边形AGPH是菱形；
（2）利用当H与D点重合时，当F点与C点重合时，分别得出x的值，进而得出答案．

解答 （1）证明：∵四边形ABCD是矩形，
∴AB∥CD，
∵AP是折痕，且延长FP交边AB于点G，
∴FG∥AH，
∴四边形AGPH是平行四边形，
∵AB∥CD，
∴∠APH=∠PAG，
∵∠PAG=∠PAG，
∴∠PAH=∠APH，
∴AH=PH，
∴平行四边形AGPH是菱形；

（2）解：当H与D点重合时，AH=AD=x=1，
当F点与C点重合时，可得AH=HC=x，
则DH=4-x，
故1²+（4-x）²=x²，
解得：x=$\frac{17}{8}$，
故x的取值范围是：1≤x≤$\frac{17}{8}$．

点评 此题主要考查了翻折变换的性质以及菱形的判定和矩形的性质等知识，正确应用矩形的性质是解题关键．