题目内容
8.观察下列运算:①由($\sqrt{2}$+1)($\sqrt{2}$-1)=1,得$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}-1$;
②由($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=1,得$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}-\sqrt{2}$;
③由($\sqrt{4}$+$\sqrt{3}$)($\sqrt{4}$-$\sqrt{3}$)=1,得$\frac{1}{\sqrt{4}+\sqrt{3}}$=2-$\sqrt{3}$;…
(1)通过观察你得出什么规律?用含n的式子表示出来.
(2)利用(1)中你发现的规律计算:
($\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}+$…+$\frac{1}{\sqrt{2016}+\sqrt{2015}}$)×($\sqrt{2016}+1$)
分析 (1)根据平方差公式,可得答案;
(2)根据分母有理化,可得二次根式的加减,根据二次根式的加减,可得答案.
解答 解:(1)规律是($\sqrt{n+1}$+$\sqrt{n}$)($\sqrt{n+1}$-$\sqrt{n}$)=1,得出$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1\sqrt{n}}$.
(2)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2016}$-$\sqrt{2015}$)($\sqrt{2016}$+1)
=($\sqrt{2016}$-1)($\sqrt{2016}$+1)
=2016-1
=2015.
点评 本题考查了分母有理化,利用平方差公式解题关键.

练习册系列答案
相关题目
1.下列调查方式合适的是( )
| A. | 为了了解一批电视机的使用寿命,采用普查方式 | |
| B. | 为了了解全国中学生的视力状况,采用普查方式 | |
| C. | 对嫦娥三号卫星零部件的检查,采用抽样调查的方式 | |
| D. | 为了了解人们保护水资源的意识,采用抽样调查的方式 |
2.在-$\frac{22}{7}$,$\root{3}{9}$,0.3,$\frac{π}{2}$,$\sqrt{25}$,$\sqrt{2}$六个数中,无理数的个数为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
17.2015年国庆节日,学校放假八日,高速公路免费通行,各地风景区游人如织.其中,闻名于西南的珠江源头风景区,在9月30日的游客人数为1000人,接下来的七天中,每天的游客人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数).
(1)10月3日的人数为1151人.
(2)假期里,游客人数最多的是10月2日,达到1209人.游客人数最少的是10月7日,达到1011人.
(3)请问珠江源头风景区在这八天内一共接待了多少游客?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 (人) | +31 | +178 | -58 | -8 | -1 | -16 | -115 |
(2)假期里,游客人数最多的是10月2日,达到1209人.游客人数最少的是10月7日,达到1011人.
(3)请问珠江源头风景区在这八天内一共接待了多少游客?
18.小华在学校组织的社会调查活动中负责了解他所居住的小区500户居民的家庭收入情况.他从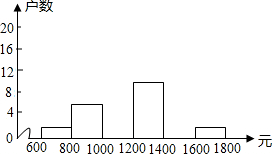 中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图.
中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图.
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数直方图.
(3)估计该居民小区家庭属于中等收入(大于等于1000不足1600元)的大约有多少户?
 中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图.
中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图. | 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | 45% | |
| 9 | 22.5% | |
| 1600≤x<1800 | 2 | |
| 合计 | 40 | 100% |
(1)补全频数分布表.
(2)补全频数直方图.
(3)估计该居民小区家庭属于中等收入(大于等于1000不足1600元)的大约有多少户?