题目内容
4．在Rt△ABC中，∠C=90°，AB=10，tanB=$\frac{1}{2}$，则S△ABC=（ ）| A． | 30 | B． | 40 | C． | 10$\sqrt{5}$ | D． | 20 |
分析 由tanB=$\frac{1}{2}$，设AC=k，BC=2k，根据勾股定理得AC2+BC2=AB2，求得k=2$\sqrt{5}$，得到AC=2$\sqrt{5}$，BC=4$\sqrt{5}$，于是得到结论．
解答 解：∵tanB=$\frac{1}{2}$，
∴设AC=k，BC=2k，
∵∠C=90°，AB=10，
∴AC2+BC2=AB2，
即：k2+（2k）2=100，
∴k=2$\sqrt{5}$，
∴AC=2$\sqrt{5}$，BC=4$\sqrt{5}$，
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}×2\sqrt{5}×4\sqrt{5}$=20．
故选D．
点评 此题考查的是锐角三角函数的定义及勾股定理的应用，三角形的面积，正确得出各边之间的关系是解决问题的关键．
练习册系列答案
相关题目
19．在平面直角坐标系xOy中，点A的坐标为（4，3），将线段OA绕原点O顺时针旋转180°，得到OA′，则点A′的坐标是（ ）
| A． | （-4，3） | B． | （-3，4） | C． | （3，-4） | D． | （-4，-3） |
9．抛物线y=x2-bx（b≠0）的顶点为C，与x轴交于A、B两点，且△ABC是等腰直角三角形，则S△ABC为（ ）
| A． | 2 | B． | 1 | C． | $\sqrt{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
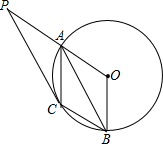如图，A、B是⊙O上的两点，∠A0B=120°，C是$\widehat{AB}$的中点． 