题目内容
16.已知a,b,c均为实数,且$\frac{ab}{a+b}=\frac{1}{3}$,$\frac{bc}{c+b}$=$\frac{1}{4}$,$\frac{ac}{c+a}$=$\frac{1}{5}$,求$\frac{abc}{ab+bc+ca}$的值.分析 已知等式左右两边求倒数,变形求出$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$的值,原式变形后代入计算即可求出值.
解答 解:由题意得:
$\frac{a+b}{ab}$=$\frac{1}{a}$+$\frac{1}{b}$=3①,
$\frac{b+c}{bc}$=$\frac{1}{b}$+$\frac{1}{c}$=4②,
$\frac{a+c}{ac}$=$\frac{1}{a}$+$\frac{1}{c}$=5③,
①+②+③得:$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$=6,
则原式=$\frac{1}{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}$=$\frac{1}{6}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图,AB为半圆O的直径,弦AD,BC相交于点P,若CD=3,AB=4,求tan∠BPD的值.
如图,AB为半圆O的直径,弦AD,BC相交于点P,若CD=3,AB=4,求tan∠BPD的值. 已知大长方形的长为10,宽为8,三个形状相同的小长方形如图放在大长方形内,则图中白色部分的面积是56.
已知大长方形的长为10,宽为8,三个形状相同的小长方形如图放在大长方形内,则图中白色部分的面积是56.
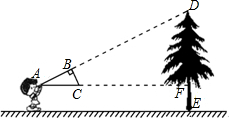 如图,小夏同学用自己做的直角三角形纸板ABC测量树的高度DE,小夏不断调整自己的位置,最终使纸板ABC的斜边AC保持水平,并且边AB与点D在同一直线上,已知纸板的两条直角边AB=0.4m,BC=0.2m,测得边AF=8m,AC离地面的高度为1.5m.求树高.
如图,小夏同学用自己做的直角三角形纸板ABC测量树的高度DE,小夏不断调整自己的位置,最终使纸板ABC的斜边AC保持水平,并且边AB与点D在同一直线上,已知纸板的两条直角边AB=0.4m,BC=0.2m,测得边AF=8m,AC离地面的高度为1.5m.求树高. 如图,△ABC≌△ADE,∠1=70°,点E正好在线段BC上,求∠FEB和∠EAC.
如图,△ABC≌△ADE,∠1=70°,点E正好在线段BC上,求∠FEB和∠EAC.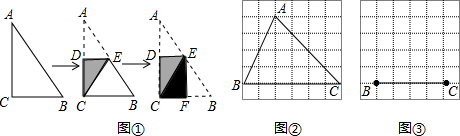
 如图,△ABC中,∠A=90°,AB=AC,BC=45,长方形DEFG为△ABC的内接长方形,且DG:DE=5:2.求DE、EF的长.
如图,△ABC中,∠A=90°,AB=AC,BC=45,长方形DEFG为△ABC的内接长方形,且DG:DE=5:2.求DE、EF的长.