题目内容
18.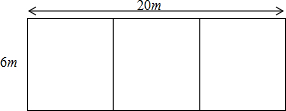 某农村为发展家庭养禽业,准备在墙外空坝上(墙长20米,空坝最窄处6米)利用现有的36米长的篱笆围成三个相连且面积相等的矩形鸡、鸭、鹅场各一个
某农村为发展家庭养禽业,准备在墙外空坝上(墙长20米,空坝最窄处6米)利用现有的36米长的篱笆围成三个相连且面积相等的矩形鸡、鸭、鹅场各一个(1)如果他要围成三个矩形总面积为72平方米,有几种围法?应选择怎样围法最合适?
(2)如果他需要围成的三个矩形总面积最大,又该怎样围?最大面积是多少?
分析 (1)设出竹篱笆围成长方形的宽为x米,则长为(36-4x)米,利用长方形的面积解答即可;
(2)设出养殖场的面积为S,考虑墙长20米,即可解决问题.
解答 解:(1)设竹篱笆围成长方形的宽为x米,则长为(36-4x)米,根据题意列方程得,
x(36-4x)=72,
解得x1=3,x2=6;
当x=3时,36-4x=24>20,不符合题意;
当x=6时,36-4x=12<20,符合题意;
∴垂直于墙的竹篱笆长6米,平行于墙的竹篱笆长12米;
答:只有1种围法;
(2)设养殖场的面积为S,充分利用墙的长20米时,围的面积最大,
根据题意得出:S=x(36-4x)=-4x2+36x=-4(x-4.5)2+81,
当x=4.5时最大,此时篱笆长36-4x=18<20米.
答:垂直于墙的竹篱笆长4.5米,平行于墙的竹篱笆长18米,最大面积81米2.
点评 考查了二次函数的应用,此题主要利用长方形的面积解答有关一元二次方程的实际应用和二次函数的实际应用,正确理解题意列出矩形的面积表达式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.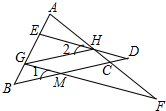 如图,已知GF⊥AB,∠1=∠2,∠AGH=∠B,则下列结论:①GH∥BC;②∠D=∠HGM;③DE∥FG;④HE⊥AB,其中正确的是( )
如图,已知GF⊥AB,∠1=∠2,∠AGH=∠B,则下列结论:①GH∥BC;②∠D=∠HGM;③DE∥FG;④HE⊥AB,其中正确的是( )
 如图,已知GF⊥AB,∠1=∠2,∠AGH=∠B,则下列结论:①GH∥BC;②∠D=∠HGM;③DE∥FG;④HE⊥AB,其中正确的是( )
如图,已知GF⊥AB,∠1=∠2,∠AGH=∠B,则下列结论:①GH∥BC;②∠D=∠HGM;③DE∥FG;④HE⊥AB,其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
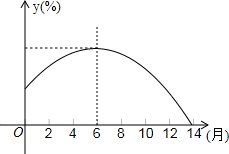 对某城市最近十几个月商品房价格涨幅情况进行调查,分析发现,与去年同期相比,房价涨幅y(%)与第x个月近似于二次函数y=-$\frac{1}{4}$x2+3x+7,如图所示,结合所学的知识,判断下列问题正确的个数为( )
对某城市最近十几个月商品房价格涨幅情况进行调查,分析发现,与去年同期相比,房价涨幅y(%)与第x个月近似于二次函数y=-$\frac{1}{4}$x2+3x+7,如图所示,结合所学的知识,判断下列问题正确的个数为( )
 如图,已知PA为⊙O的切线,割线PB交圆于B,C两点,连PO,AD⊥PO于D点,连接CD,BO,求证:∠PDC=∠PBO.
如图,已知PA为⊙O的切线,割线PB交圆于B,C两点,连PO,AD⊥PO于D点,连接CD,BO,求证:∠PDC=∠PBO.