题目内容
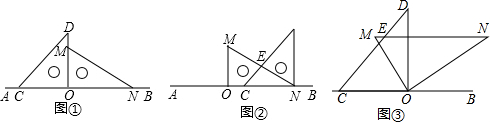
6.如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;
(3)将图①中的三角板OMN绕点O按每秒30°的速度按逆时针方向旋转一周,在旋转的过程中,在第5.5或11.5秒时,直线MN恰好与直线CD垂直.(直接写出结果)
分析 (1)根据三角形的内角和定理列式计算即可得解;
(2)根据内错角相等,两直线平行判断出MN∥BC,再根据两直线平行,同旁内角互补解答;
(3)作出图形,然后分两种情况求出旋转角,再根据时间=旋转角÷速度计算即可得解.
解答 解:(1)在△CEN中,∠CEN=180°-30°-45°=105°;
(2)∵∠BON=∠N=30°,
∴MN∥BC,
∴∠CEN=180°-∠DCO=180°-45°=135°;
(3)如图,MN⊥CD时,旋转角为90°+(180°-60°-45°)=165°,
或360°-(60°-45°)=345°,
所以,t=165°÷30°=5.5秒,
或t=345°÷30°=11.5秒.
故答案为:5.5或11.5.
点评 本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,分情况讨论,作出图形是解答此题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
14.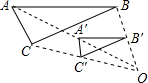 如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )
如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )
 如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )
如图,位似中心为O,将△ABC经过位似变换后得到位似图形△A′B′C′,当AB=2A′B′时,位似比k的值为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 不确定 |
16.下表是丁老师家9月份连续8天每天中午电表的读数:
请你估计丁老师家9月份(30天)的用电量是157.5kW•h.
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电表读数 (kW•h) | 25 | 31 | 35 | 40 | 47 | 55 | 61 | 67 |
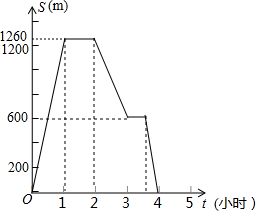 张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿返回,途中在读报栏前看了一会儿报,此情景如图所示,请你回答下列问题:
张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿返回,途中在读报栏前看了一会儿报,此情景如图所示,请你回答下列问题: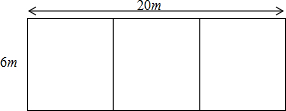 某农村为发展家庭养禽业,准备在墙外空坝上(墙长20米,空坝最窄处6米)利用现有的36米长的篱笆围成三个相连且面积相等的矩形鸡、鸭、鹅场各一个
某农村为发展家庭养禽业,准备在墙外空坝上(墙长20米,空坝最窄处6米)利用现有的36米长的篱笆围成三个相连且面积相等的矩形鸡、鸭、鹅场各一个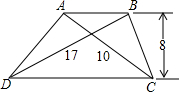 如图所示,梯形的两条对角线分别为10cm和17cm,高为8cm,求这个梯形的面积.
如图所示,梯形的两条对角线分别为10cm和17cm,高为8cm,求这个梯形的面积.