题目内容
4. 如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=6cm,求AD的长.
如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=6cm,求AD的长.
分析 根据等边对等角可得∠B=∠C,再利用三角形的内角和定理求出∠BAC=120°,然后求出∠CAD=30°,从而得到∠CAD=∠C,根据等角对等边可得AD=CD,再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2AD,然后根据BC=BD+CD列出方程求解即可.
解答 解:∵AB=AC,
∴∠B=∠C=30°,
∴∠BAC=180°-2×30°=120°,
∵DA⊥BA,
∴∠BAD=90°,
∴∠CAD=120°-90°=30°,
∴∠CAD=∠C,
∴AD=CD,
在Rt△ABD中,∵∠B=30°,∠BAD=90°,
∴BD=2AD,
∴BC=BD+CD=2AD+AD=3AD,
∵BC=6cm,
∴AD=2cm.
点评 本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,等角对等边和等边对等角的性质,熟记性质并准确识图,用AD表示出BC是解题的关键.

练习册系列答案
相关题目
15.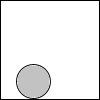 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )| A. | a2-π | B. | 4-π | C. | π | D. | (4-π)a2 |
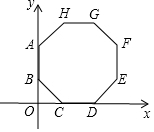 如图,正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).
如图,正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).