题目内容
二次函数y=ax2+bx+c(a、b、c为常数且(a≠0)中的x与y的部分对应值如表
给出了结论:
(1)二次函数y=ax2+bx+c有最大值,最大值为4;
(2)若-1<x<2时,y>0;
(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧;
(4)2a+b=0
则其中正确结论的个数是( )
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | -12 | -5 | 0 | 3 | 4 | 3 | 0 | -5 | -12 |
(1)二次函数y=ax2+bx+c有最大值,最大值为4;
(2)若-1<x<2时,y>0;
(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧;
(4)2a+b=0
则其中正确结论的个数是( )
| A、4 | B、3 | C、2 | D、1 |
考点:二次函数的性质
专题:
分析:利用题目中所给数据可求得二次函数的解析式,再逐个判断即可.
解答:解:
由表中所给数值可知当x=-1或3时,y=0,当x=0时,y=3,代入二次函数的解析式可得
,解得
,
∴二次函数的解析式为y=-x2+2x+3=-(x-1)2+4,
∴当x=1时有最大值4,
∴(1)正确;
二次函数开口向下,与x轴的两个交点为(-1,0)和(3,0),
∴当-1<x<3时,y>0,
∴(2)、(3)正确;
对称轴为x=1,即-
=1,整理可得2a+b=0,
∴(4)正确;
综上可知正确的结论有四个,
故选A.
由表中所给数值可知当x=-1或3时,y=0,当x=0时,y=3,代入二次函数的解析式可得
|
|
∴二次函数的解析式为y=-x2+2x+3=-(x-1)2+4,
∴当x=1时有最大值4,
∴(1)正确;
二次函数开口向下,与x轴的两个交点为(-1,0)和(3,0),
∴当-1<x<3时,y>0,
∴(2)、(3)正确;
对称轴为x=1,即-
| b |
| 2a |
∴(4)正确;
综上可知正确的结论有四个,
故选A.
点评:本题主要考查二次函数的性质,利用待定系数法求得二次函数的解析式是解题的关键.注意二次函数一般式化为顶点式的方法.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,AC=6,BC=8,则sinB的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知如图:等边△ABC中,D是AB上一点,∠EDF=60°,则∠AED=( )
已知如图:等边△ABC中,D是AB上一点,∠EDF=60°,则∠AED=( )| A、t∠B | B、∠BFD |
| C、∠ADE | D、∠BDF |
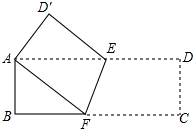 如图,ABCD是一张长方形纸片,AB=CD=3,BC=AD=9.在边AD上取一点E,在BC上取一点F,将纸片沿EF折叠,点C恰好落在点A处,则线段EF的长度为
如图,ABCD是一张长方形纸片,AB=CD=3,BC=AD=9.在边AD上取一点E,在BC上取一点F,将纸片沿EF折叠,点C恰好落在点A处,则线段EF的长度为



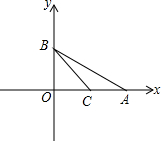 在平面直角坐标系中,点A、点C在x轴的正半轴上,点B在y轴的正半轴上,且A(a,0),B(0,b),C(c,0),b2+2ab=c2+2ac,判断△BOC的形状,并证明.
在平面直角坐标系中,点A、点C在x轴的正半轴上,点B在y轴的正半轴上,且A(a,0),B(0,b),C(c,0),b2+2ab=c2+2ac,判断△BOC的形状,并证明.