题目内容
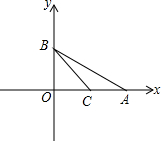 在平面直角坐标系中,点A、点C在x轴的正半轴上,点B在y轴的正半轴上,且A(a,0),B(0,b),C(c,0),b2+2ab=c2+2ac,判断△BOC的形状,并证明.
在平面直角坐标系中,点A、点C在x轴的正半轴上,点B在y轴的正半轴上,且A(a,0),B(0,b),C(c,0),b2+2ab=c2+2ac,判断△BOC的形状,并证明.考点:因式分解的应用,坐标与图形性质
专题:
分析:由点A、点C在x轴的正半轴上,点B在y轴的正半轴上,得出a、b、c都是正数,进一步把b2+2ab=c2+2ac,因式分解,探讨得出a、b、c三者之间的关系,进一步判定△BOC的形状即可.
解答:解:∵点A、点C在x轴的正半轴上,点B在y轴的正半轴上,
∴a>0,b>0,c>0,
∵b2+2ab=c2+2ac,
∴(b-c)(2a+b+c)=0,
∴b-c=0,
∴b=c,
即OB=OC,
∴△BOC为等腰直角三角形.
∴a>0,b>0,c>0,
∵b2+2ab=c2+2ac,
∴(b-c)(2a+b+c)=0,
∴b-c=0,
∴b=c,
即OB=OC,
∴△BOC为等腰直角三角形.
点评:此题考查因式分解的运用,注意题目条件的理解与运用,结合图形灵活解决问题.

练习册系列答案
相关题目
两个有理数a,b,|a|<|b|,并且a>0,b<0,则下列各式正确的是( )
| A、-a<b<a<-b |
| B、b<-a<a<-b |
| C、-a<-b<b<a |
| D、b<-a<-b<a |