题目内容
7. 如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E.
如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E.(1)若AD⊥BC于D,∠C=40°,求∠DAE的度数;
(2)若EF⊥AE交AC于F,求证:∠C=2∠FEC.
分析 (1)首先计算出∠B,∠BAC的度数,然后可得∠EAC=30°,再根据直角三角形两锐角互余可得∠DAC的度数,进而可得答案;
(2)首先证明∠DAE=∠FEC,然后再根据三角形内角和定理可得∠EAC=90°-$\frac{3}{2}$∠C,再利用角之间的和差关系可得∠DAE=∠DAC-∠EAC,利用等量代换可得∠DAE=$\frac{1}{2}∠$C,进而可得结论.
解答 (1)解:∵∠C=40°,∠B=2∠C,
∴∠B=80°,
∴∠BAC=60°,
∵AE平分∠BAC,
∴∠EAC=30°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=50°,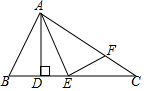
∴∠DAE=50°-30°=20°;
(2)证明:∵EF⊥AE,
∴∠AEF=90°,
∴∠AED+∠FEC=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∵AE平分∠BAC,
∴∠EAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=$\frac{1}{2}$(180°-3∠C)=90°-$\frac{3}{2}$∠C,
∵∠DAE=∠DAC-∠EAC,
∴∠DAE=∠DAC-(90°-$\frac{3}{2}$∠C)=90°-∠C-90°+$\frac{3}{2}$∠C=$\frac{1}{2}$∠C,
∴∠FEC=$\frac{1}{2}∠$C,
∴∠C=2∠FEC.
点评 此题主要考查了三角形内角和定理,关键是掌握三角形内角和为180°,直角三角形两锐角互余.

练习册系列答案
相关题目
12.上周五某股民买进一只股票1000股,每股55元,如表为本周内每日股票的涨跌情况(单位:元)
他本周五收盘时把股票全部卖掉,求他的获利情况.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +4 | -5 | +4.5 | -2 | +2.5 |
17.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
已知日销售量y是售价x的一次函数.
(1)直接写出日销售量y(件)与销售价x(元)的函数关系.
(2)要使每日的销售利润最大,每件产品的售价应定为多少元?此时的日销售利润是多少?若日销售利润低于125元且不亏本,请直接写出售价的取值范围.
| x(元) | 15 | 20 | 30 | … |
| y(件) | 25 | 20 | 10 | … |
(1)直接写出日销售量y(件)与销售价x(元)的函数关系.
(2)要使每日的销售利润最大,每件产品的售价应定为多少元?此时的日销售利润是多少?若日销售利润低于125元且不亏本,请直接写出售价的取值范围.
 如图,在Rt△ABC中,AD为斜边BC上的高,∠ABC的平分线BE交AC于E,交AD于F.
如图,在Rt△ABC中,AD为斜边BC上的高,∠ABC的平分线BE交AC于E,交AD于F. 已知三角形ABC的面积为96平方厘米,BC=3DC,FD=2AF,求三角形AEF的面积.
已知三角形ABC的面积为96平方厘米,BC=3DC,FD=2AF,求三角形AEF的面积.