题目内容
2. 已知三角形ABC的面积为96平方厘米,BC=3DC,FD=2AF,求三角形AEF的面积.
已知三角形ABC的面积为96平方厘米,BC=3DC,FD=2AF,求三角形AEF的面积.
分析 连接DE,因为三角形ABC的面积为96平方厘米,BC=3DC,根据高一定时,三角形的面积与底成正比例的性质可得,三角形ACD=32,三角形ADB=64;
且三角形BDE的面积=三角形CDE的面积的2倍;由FD=2AF,可得:三角形AFB=$\frac{64}{3}$,三角形DFB=$\frac{128}{3}$;且三角形AEF的面积=$\frac{1}{2}$三角形DEF的面积,由此设三角形AEF=三角形DEF的面积为x,则根据等量关系:“三角形CDE的面积=三角形BDE的面积的2倍”列出方程即可解决问题.
解答 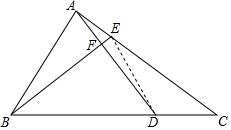 解:连接DE,因为三角形ABC的面积为96平方厘米,BC=3DC,
解:连接DE,因为三角形ABC的面积为96平方厘米,BC=3DC,
所以三角形ACD=32,三角形ADB=64;
且三角形BDE的面积=三角形CDE的面积的2倍;
由FD=2AF,可得:三角形AFB=$\frac{64}{3}$,三角形DFB=$\frac{128}{3}$;且三角形AEF的面积=$\frac{1}{2}$三角形DEF的面积,
设三角形AEF的面积为x,根据图形可得:
$\frac{128}{3}$+2x=2(32-3x),
解得x=$\frac{8}{3}$.
答:三角形AEF的面积是$\frac{8}{3}$.
点评 此题考查了三角形的面积,反复利用了高一定时,三角形的面积与底成正比例的性质的灵活应用.

练习册系列答案
相关题目
 已知:如图,AB是⊙O的直径,弦CD⊥AB,M为AC上一点,AM的延长线交DC的延长线于F,求证:∠AMD=∠FMC.
已知:如图,AB是⊙O的直径,弦CD⊥AB,M为AC上一点,AM的延长线交DC的延长线于F,求证:∠AMD=∠FMC. 如图在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点N,求证:
如图在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点N,求证: 如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E.
如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E.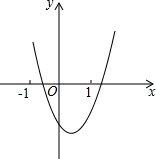 二次函数y=ax2+bx+c的图象如图所示,请写出一次函数y=bx+b2-4ac与反比例函数y=$\frac{a+b+c}{x}$的图象分别经过哪几个象限?并说明理由.
二次函数y=ax2+bx+c的图象如图所示,请写出一次函数y=bx+b2-4ac与反比例函数y=$\frac{a+b+c}{x}$的图象分别经过哪几个象限?并说明理由.