题目内容
16.计算:(1)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$;
(2)($\frac{1}{\sqrt{5}}$)-1-$\frac{1}{3}$$\sqrt{45}$+|4-2$\sqrt{5}$|-$\sqrt{20}$;
(3)3$\sqrt{\frac{1}{3}}$-$\sqrt{(\sqrt{3}-2)^{2}}$-6$\sqrt{2}$÷$\sqrt{\frac{3}{2}}$.
分析 (1)利用多项式与单项式的除法法则即可求解;
(2)首先计算负指数次幂,去掉绝对值符号,化简二次根式,然后合并同类二次根式即可;
(3)去掉绝对值符号,化简二次根式,然后合并同类二次根式即可.
解答 解:(1)原式=$\frac{3\sqrt{4}}{2}$-$\frac{1}{4}$$\sqrt{\frac{1}{9}}$+$\frac{\sqrt{16}}{2}$=3-$\frac{1}{12}$+2=5-$\frac{1}{12}$=$\frac{59}{12}$;
(2)原式=$\sqrt{5}$-$\sqrt{5}$+2$\sqrt{5}$-4-2$\sqrt{5}$=-4;
(3)原式=$\sqrt{3}$-(2-$\sqrt{3}$)-6$\sqrt{\frac{4}{3}}$=$\sqrt{3}$-2+$\sqrt{3}$-4$\sqrt{3}$=-2-2$\sqrt{3}$.
点评 本题考查了二次根式的化简求值,正确根据式子的特点确定正确的运算顺序是关键.

练习册系列答案
相关题目
6.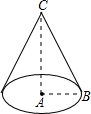 如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )
如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )
 如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )
如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )| A. | 10π | B. | 12π | C. | 14π | D. | 16π |
 如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E.
如图,在△ABC中,∠B=2∠C,AE平分∠BAC交BC于E. 如图,用12米长的铝合金做一个有横档的矩形窗子,横档长为x,矩形窗子的宽为y,则y关于x的函数解析式为y=-1.5x+6.
如图,用12米长的铝合金做一个有横档的矩形窗子,横档长为x,矩形窗子的宽为y,则y关于x的函数解析式为y=-1.5x+6.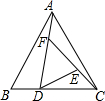 如图,在△ABC中,已知△ABC的面积为1,BD=$\frac{1}{2}$DC,AF=$\frac{1}{2}$FD,CE=$\frac{1}{2}$EF,求△DEF的面积.
如图,在△ABC中,已知△ABC的面积为1,BD=$\frac{1}{2}$DC,AF=$\frac{1}{2}$FD,CE=$\frac{1}{2}$EF,求△DEF的面积.