题目内容
14.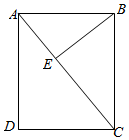 如图,矩形ABCD中,AB=6,BE⊥AC于E,sin∠EBC=$\frac{4}{5}$,求矩形ABCD的面积.
如图,矩形ABCD中,AB=6,BE⊥AC于E,sin∠EBC=$\frac{4}{5}$,求矩形ABCD的面积.
分析 根据矩形的性质知:∠D=90°,CD=AB,在Rt△ADC中,已知sin∠DCA和CD的值,运用三角函数可将AD的长求出,代入S矩形ABCD=AB×AD进行求解即可.
解答 解:由矩形的性质知:∠D=90°,CD=AB=6,sin∠EBC=$\frac{4}{5}$,
在Rt△ADC中,sin∠DCA=$\frac{4}{5}$,
∴tan∠DCA=$\frac{4}{3}$,AD=tan∠DCA×CD=8
∴S矩形ABCD=AD×AB=8×6=48.
点评 本题主要考查解直角三角形问题,关键是根据矩形的性质和三角函数在解直角三角形中的应用解答.

练习册系列答案
相关题目
6.-(-3)、-(+2)的化简结果为( )
| A. | -3、-2 | B. | 3、-2 | C. | -3、2 | D. | 3、2 |
 若用A、B、C、D分别表示有理数a、b、c,0为原点如图所示.已知a<c<0,b>0.
若用A、B、C、D分别表示有理数a、b、c,0为原点如图所示.已知a<c<0,b>0.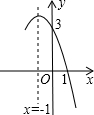 抛物线y=-x2+bx+c的部分图象如图所示,则-x2+bx+c>0的解集是-3<x<1.
抛物线y=-x2+bx+c的部分图象如图所示,则-x2+bx+c>0的解集是-3<x<1. 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.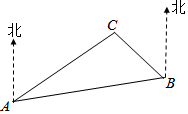 如图是A,B,C三岛的平面图,C岛在A岛的北偏东60°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向.求从C岛看A,B两岛的视角∠ACB的度数.
如图是A,B,C三岛的平面图,C岛在A岛的北偏东60°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向.求从C岛看A,B两岛的视角∠ACB的度数.