题目内容
3.某公司经销一种商品,每件成本为20元.经市场调查发现,在一段时间内,销售量w(件)随销售单价x(元/件)的变化而变化,具体关系式为:w=-10x+500.设这种商品在这段时间内的销售利润为y(元),解答下列问题:(1)求y与x的函数关系式;
(2)当x取何值时,利润最大?最大利润为多少元?
(3)如果物价部门规定这种商品的销售单价不得高于32元/件,公司想要在这段时间内获得2000元的销售利润,销售单价应定为多少元?
分析 (1)根据总利润=单件利润×销售量可得;
(2)根据二次函数的性质可得;
(3)根据题意列出方程求解,再结合题意取舍即可.
解答 解:①y=(x-20)(-10x+500)=-10x2+700x-10000;
②当x=-$\frac{700}{2×10}$=35时 y最大值=2250;
③根据题意可得:-10x2+700x-1000=2000,
解得:x1=30,x2=40.
∵x≤32,
∴x=40,
答:销售单价应定为40元.
点评 本题主要考查二次函数的应用,理解题意抓住相等关系列出方程或函数解析式是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
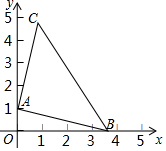 如图,已知点A(0,1),点B是x轴正半轴上一动点,以AB为边作等腰直角三角形ABC,使点C在第一象限,∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,则表示y与x的函数关系的图象大致是( )
如图,已知点A(0,1),点B是x轴正半轴上一动点,以AB为边作等腰直角三角形ABC,使点C在第一象限,∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,则表示y与x的函数关系的图象大致是( )



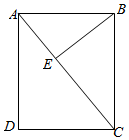 如图,矩形ABCD中,AB=6,BE⊥AC于E,sin∠EBC=$\frac{4}{5}$,求矩形ABCD的面积.
如图,矩形ABCD中,AB=6,BE⊥AC于E,sin∠EBC=$\frac{4}{5}$,求矩形ABCD的面积.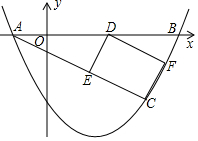 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c图象经过A(-1,0),B(4,0)两点.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c图象经过A(-1,0),B(4,0)两点. 若实数a、b、c在数轴上的对应点如图所示,试化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$+|b+c|+|a-c|.
若实数a、b、c在数轴上的对应点如图所示,试化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$+|b+c|+|a-c|.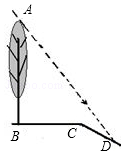 如图,坡面CD的坡比为1:$\sqrt{3}$,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=$\sqrt{3}$米,求小树AB的高.
如图,坡面CD的坡比为1:$\sqrt{3}$,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=$\sqrt{3}$米,求小树AB的高.