题目内容
15.已知点A(-1,-2),B关于抛物线y=a(x-1)2的对称轴对称,则点B的坐标为( )| A. | (1,-2) | B. | (-1,2) | C. | (2,-2) | D. | (3,-2) |
分析 由条件可求得抛物线对称轴,再利用对称性可求得B点坐标.
解答 解:
∵y=a(x-1)2,
∴对称轴为x=1,
∵点A、B关于对称轴对称,
∴A、B两点到对称轴的距离相等,且纵坐标相同,
∴B点横坐标为x=2×1-(-1)=3,纵坐标为-2,
∴B(3,-2),
故选D.
点评 本题主要考查二次函数的性质,掌握二次函数的对称性是解题的关键.

练习册系列答案
相关题目
5.有如下四个事件:①篮球队员在罚球线上投篮一次,未投中;②任意画一个圆的内接四边形,这个四边形的对角互补;③经过有交通信号灯的路口,遇到红灯;④三角形的外心落在三角形的内部.上述事件中是随机事件的是( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
6.方程(x-1)(x+2)=x-1的解是( )
| A. | -2 | B. | 1,-2 | C. | -1,1 | D. | -1,3 |
3. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解为( )| A. | x>-1 | B. | x<-2 | C. | x<-1 | D. | 无法确定 |
10.如果不等式组$\left\{\begin{array}{l}{x+7<3x-7}\\{x>n}\end{array}\right.$的解集是x>7,则n的取值范围是( )
| A. | n=7 | B. | n<7 | C. | n≥7 | D. | n≤7 |
20.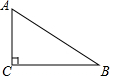 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=4cm,若以点C为圆心,以2cm为半径作⊙C,则AB与⊙C的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相切或相交 |
7.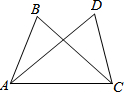 如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
 如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
如图,己知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )| A. | BC=AD | B. | ∠B=∠D=90° | C. | ∠BAC=∠CAD | D. | ∠ACB=∠CAD |
4.方程x2-x=0的解是( )
| A. | x=0 | B. | x=1 | C. | x1=0,x2=1 | D. | x1=0,x2=-1 |
5.点P位于y轴左侧,距y轴3个单位,且位于x轴下方,距x轴5个单位,则点P位的坐标为( )
| A. | (-3,-5) | B. | (-3,5) | C. | (5,-3) | D. | (-5,-3) |