题目内容
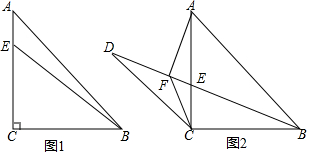
5.如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.(1)如图1,若AB=4$\sqrt{2}$,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.
分析 (1)根据等腰直角三角形的性质得到AC=BC=$\frac{\sqrt{2}}{2}$AB=4,根据勾股定理得到CE=$\sqrt{B{E}^{2}-B{C}^{2}}$=3,于是得到结论;
(2)根据等腰直角三角形的性质得到∠CAB=45°,由于∠AFB=∠ACB=90°,推出A,F,C,B四点共圆,根据圆周角定理得到∠CFB=∠CAB=45°,求得∠DFC=∠AFC=135°,根据全等三角形的性质即可得到结论.
解答 解:(1)∵∠ACB=90°,AC=BC,
∴AC=BC=$\frac{\sqrt{2}}{2}$AB=4,
∵BE=5,
∴CE=$\sqrt{B{E}^{2}-B{C}^{2}}$=3,
∴AE=4-3=1;
(2)∵∠ACB=90°,AC=BC,
∴∠CAB=45°,
∵AF⊥BD,
∴∠AFB=∠ACB=90°,
∴A,F,C,B四点共圆,
∴∠CFB=∠CAB=45°,
∴∠DFC=∠AFC=135°,
在△ACF与△DCF中,$\left\{\begin{array}{l}{AF=DF}\\{∠AFC=∠DFC}\\{CF=CF}\end{array}\right.$,
∴△ACF≌△DCF,
∴CD=AC,
∵AC=BC,
∴AC=BC.
点评 本题考查了全等三角形的判定和性质,四点共圆,等腰直角三角形的性质,勾股定理,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
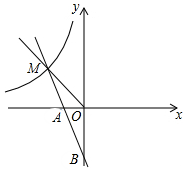 如图,一次函数y=kx+b的图象经过A(-1,0),B(0,-2)l两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是3.
如图,一次函数y=kx+b的图象经过A(-1,0),B(0,-2)l两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是3.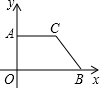 如图,在平面直角坐标系xOy中,点A、B的坐标分别为(0,3)、(7,0),点C在第一象限,AC∥x轴,∠OBC=45°.
如图,在平面直角坐标系xOy中,点A、B的坐标分别为(0,3)、(7,0),点C在第一象限,AC∥x轴,∠OBC=45°.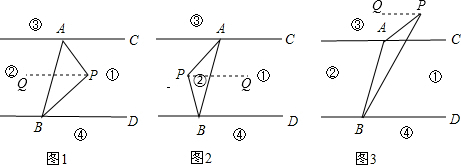
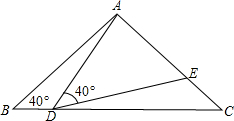 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E. 如图,已知AC∥ED,AB∥FD,∠A=55°,求∠EDF的度数.
如图,已知AC∥ED,AB∥FD,∠A=55°,求∠EDF的度数.
 如图,测量河宽AB(河的两岸平行),在C点测得∠ACB=32°,BC=60m,则河宽AB约为37.5m.(用科学计算器计算,结果精确到0.1)
如图,测量河宽AB(河的两岸平行),在C点测得∠ACB=32°,BC=60m,则河宽AB约为37.5m.(用科学计算器计算,结果精确到0.1)