题目内容
14．解不等式组：$\left\{{\begin{array}{l}{3x+1≥2x}\\{4（x-1）＜2x}\end{array}}\right.$，并把解集在数轴上表示出来．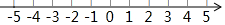
分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：不等式组：$\left\{\begin{array}{l}{3x+1≥2x}&{①}\\{4（x-1）＜2x}&{②}\end{array}\right.$，
由①得：x≥-1，
由②得：x＜2，
∴不等式组的解是-1≤x＜2，
在数轴上表示：
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
2．
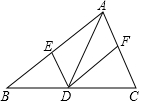在△ABC中，点D是边BC上的点（与B，C两点不重合），过点D作DE∥AC，DF∥AB，分别交AB，AC于E，F两点，下列说法正确的是（ ）
在△ABC中，点D是边BC上的点（与B，C两点不重合），过点D作DE∥AC，DF∥AB，分别交AB，AC于E，F两点，下列说法正确的是（ ）| A． | 若AD⊥BC，则四边形AEDF是矩形 | |
| B． | 若AD垂直平分BC，则四边形AEDF是矩形 | |
| C． | 若BD=CD，则四边形AEDF是菱形 | |
| D． | 若AD平分∠BAC，则四边形AEDF是菱形 |
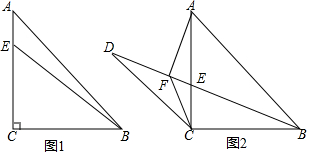
如图，某教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2m的影子CE；而当光线与地面夹角是45°时，教学楼顶部A在地面上的影子F与墙角C的距离为18m（B、F、C在同一直线上）．求教学楼AB的高；（结果保留整数）（参考数据：sim22°≈0.37，cos22°≈0.93，tan22°≈0.40）
公路施工中需要建设穿过小山的隧道DE，采用从两边同时施工的方法，甲工程队从D向E施工，乙工程队从E向D施工，为了使两工程队施工能在山中对接，需要保证A，D，E，C，在同一直线上．为此，在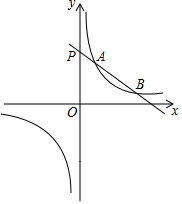
如图，反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A，B两点，点A的坐标为（2，6），点B的坐标为（n，1），且与y轴交于点P．
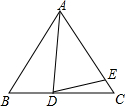已知△ABC，AB=AC，D为直线BC上一点，E为直线AC上一点，AD=AE，设∠BAD=α，∠CDE=β．
4．下列运算中，正确的是（ ）
| A． | （x+1）2=x2+1 | B． | （x2）3=x5 | C． | 2x4•3x2=6x8 | D． | x2÷x-1=x3（x≠0） |