题目内容
如图，AB⊥AC，AD⊥BC，已知AB=6，BC=9，则图中线段的长BD=考点：射影定理
专题：计算题
分析：根据射影定理得AB2=BD•BC，则可计算出BD=4，再计算出CD=BC-BD=5，然后根据AD2=BD•CD计算出AD，利用AC2=CD•BC计算出AC．
解答：解：∵AB⊥AC，AD⊥BC，
∴AB2=BD•BC，即62=BD•9，解得BD=4，
∴CD=BC-BD=5，
∵AD2=BD•CD，
∴AD=
=2
，
∵AC2=CD•BC，
∴AC=
=3
．
故答案为4，2
，3
．
∴AB2=BD•BC，即62=BD•9，解得BD=4，
∴CD=BC-BD=5，
∵AD2=BD•CD，
∴AD=
| 4×5 |
| 5 |
∵AC2=CD•BC，
∴AC=
| 5×9 |
| 5 |
故答案为4，2
| 5 |
| 5 |
点评：本题考查了射影定理：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项；每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．
练习册系列答案
相关题目
一组数据：2，4，5，6，x的平均数是4，则这组数的标准差是（ ）
| A、2 | ||
B、
| ||
| C、10 | ||
D、
|
下列运算正确的是（ ）
| A、a2a3=a6 |
| B、2x2-x2=1 |
| C、8x4÷（-4x）=-2x3 |
| D、a3=3a |
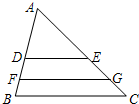如图，点D、E、F、G为△ABC两边上的点，且DE∥FG∥BC，若DE、FG将△ABC的面积三等分，那么下列结论正确的是（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
用频率估计概率，可以发现，抛掷硬币，“正面朝上”的概率为0.5，是指（ ）
| A、连续掷2次，结果一定是“正面朝上”和“反面朝上”各1次 |
| B、连续抛掷100次，结果一定是“正面朝上”和“反面朝上”各50次 |
| C、抛掷2n次硬币，恰好有n次“正面朝上” |
| D、抛掷n次，当n越来越大时，正面朝上的频率会越来越稳定于0.5 |
已知a=255，b=344，c=433，则a、b、c的大小关系是（ ）
| A、b＞c＞a |
| B、a＞b＞c |
| C、c＞a＞b |
| D、a＜b＜c |
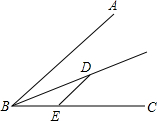如图，∠ABC=50°，BD平分∠ABC，过D作DE∥AB交BC于点E，若点F在AB上，且满足DF=DE，则∠DFB的度数为（ ）| A、25° |
| B、130° |
| C、50°或130° |
| D、25°或130° |
下列说法：①-5是25的平方根；②36的平方根是6；③
的算术平方根是4；④算术平方根等于它本身的数是0或1，其中正确的有（ ）
| 16 |
| A、1个 | B、2个 | C、3个 | D、4个 |