题目内容
14.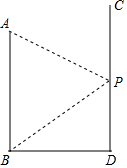 如图,AB、CD分别表示两幢相距36米的大楼,高兴同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°,求大楼AB的高.
如图,AB、CD分别表示两幢相距36米的大楼,高兴同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°,求大楼AB的高.
分析 过点P作AB 的垂线,垂足为E,根据题意可得出四边形PDBE是矩形,再由∠EPB=45°可知BE=PE=36m,由AE=PE•tan30°得出AE的长,进而可得出结论.
解答  解:如图,过点P作AB 的垂线,垂足为E,
解:如图,过点P作AB 的垂线,垂足为E,
∵PD⊥AB,DB⊥AB,
∴四边形PDBE是矩形,
∵BD=36m,∠EPB=45°,
∴BE=PE=36m,
∴AE=PE•tan30°=36×$\frac{\sqrt{3}}{3}$=12$\sqrt{3}$(m),
∴AB=12$\sqrt{3}$+36(m).
答:建筑物AB的高为$36+12\sqrt{3}$米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
4.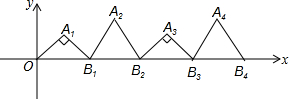 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )| A. | (4029,1) | B. | (2015,$\sqrt{3}$) | C. | (4030,1) | D. | (4029,$\sqrt{3}$) |
5.将235000000用科学记数法表示为( )
| A. | 235×106 | B. | 2.35×107 | C. | 2.35×108 | D. | 0.235×109 |
19.如果在Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式正确的是( )
| A. | tanB=$\frac{2}{3}$ | B. | cotB=$\frac{2}{3}$ | C. | sinB=$\frac{2}{3}$ | D. | cosB=$\frac{2}{3}$ |
9.若(ax+3y)2=4x+12xy-by2,则a、b的值依次为( )
| A. | -2、9 | B. | -4、9 | C. | 2、9 | D. | 2、-9 |