题目内容
9.在三个整式x2-1,x2+2x+1,x2+x中,请你从中任意选择两个,将其中一个作为分子、另一个作为分母组成一个分式,并将这个分式进行化简,再从-2<x<2的范围内选取合适的整数作为x的值代入分式求值.分析 先根据题意得出分式,再根据分式混合运算的法则把原式进行化简,再选出合适的x的值代入进行计算即可.
解答 解:选择整式x2-1为分子,x2+2x+1为分母组成分式,
原式=$\frac{{x}^{2}-1}{{x}^{2}+2x+1}$
=$\frac{(x+1)(x-1)}{(x+1)^{2}}$
=$\frac{x-1}{x+1}$,
当x=0时,原式=$\frac{-1}{1}$=-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
19.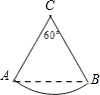 如图,圆心角为60°的扇形中,弦AB=4,则扇形面积为( )
如图,圆心角为60°的扇形中,弦AB=4,则扇形面积为( )
 如图,圆心角为60°的扇形中,弦AB=4,则扇形面积为( )
如图,圆心角为60°的扇形中,弦AB=4,则扇形面积为( )| A. | 2π | B. | $\frac{8}{3}$π | C. | 2$\sqrt{3}$π | D. | 6π |
20. 如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D=( )
如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D=( )
 如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D=( )
如图,AD∥BC,BD平分∠ABC,且∠A=110°,则∠D=( )| A. | 55° | B. | 70° | C. | 90° | D. | 35° |
4.下列四个数中,比0小的是( )
| A. | -2 | B. | 1 | C. | $\sqrt{3}$ | D. | 4 |
14.下列汽车图案中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.1不是-1的( )
| A. | 平方数 | B. | 倒数 | C. | 相反数 | D. | 绝对值 |
18. 如图所示,P是⊙O的弦AB上的一点,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( )cm.
如图所示,P是⊙O的弦AB上的一点,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( )cm.
 如图所示,P是⊙O的弦AB上的一点,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( )cm.
如图所示,P是⊙O的弦AB上的一点,AB=10cm,AP=4cm,OP=5cm,则⊙O的半径为( )cm.| A. | 5 | B. | 7 | C. | 6 | D. | 6.5 |
 已知,如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥DC.求证:DC=CB.
已知,如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥DC.求证:DC=CB.