题目内容
19.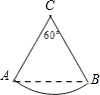 如图,圆心角为60°的扇形中,弦AB=4,则扇形面积为( )
如图,圆心角为60°的扇形中,弦AB=4,则扇形面积为( )| A. | 2π | B. | $\frac{8}{3}$π | C. | 2$\sqrt{3}$π | D. | 6π |
分析 过点C作CD⊥AB于点D,由垂径定理求出AD的长,再根据直角三角形的性质求出AC的长,由扇形的面积公式即可得出结论.
解答  解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
∵AB=4,∠ACB=60°,
∴AD=2,∠ACD=30°,
∴AC=2AD=4,
∴S扇形ACB=$\frac{60π×{4}^{2}}{360}$=$\frac{60π×16}{360}$=$\frac{8}{3}$π.
故选B.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
9.下列计算正确的是( )
| A. | 2a5+a5=3a10 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a10÷a2=a8 |
4.若将函数y=2x2的图象向右平行移动5个单位,再向上平移1个单位,可得到的抛物线是( )
| A. | y=2(x-5)2+1 | B. | y=2(x-5)2-1 | C. | y=2(x+5)2-1 | D. | y=2(x+5)2+1 |
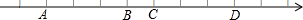 如图,已知数轴上A,B,C,D四点对应的实数都是整数,若A对应的实数为a,B对应的实数为b,且b-2a=7,那么数轴的原点应是( )
如图,已知数轴上A,B,C,D四点对应的实数都是整数,若A对应的实数为a,B对应的实数为b,且b-2a=7,那么数轴的原点应是( )