题目内容
12．
如图，以点O为位似中心，将△ABC放大得到△DEF，若AD=OA，则△ABC与△DEF的面积之比为1：4．
分析 由AD=OA，易得△ABC与△DEF的位似比等于1：2，继而求得△ABC与△DEF的面积之比．
解答 解：∵以点O为位似中心，将△ABC放大得到△DEF，AD=OA，
∴AB：DE=OA：OD=1：2，
∴△ABC与△DEF的面积之比为：1：4．
故答案为：1：4．
点评 此题考查了位似图形的性质．注意相似三角形的面积比等于相似比的平方．
练习册系列答案
相关题目
如图，正△ABC与正△A1B1C1关于某点中心对称，已知A，A1，B三点的坐标分别是（0，4），（0，3），（0，2）．
20．下列图形中，是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
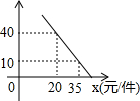学生小李在暑假进行社会实践活动，准备采购一批学习用品进行销售，进货时老板告诉小李，每件商品可以优惠2元，这样原价330元的商品现在可以多买1件还余10元．
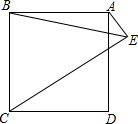如图，若点E为正方形ABCD外一点，∠BEC=45°，连接AE．
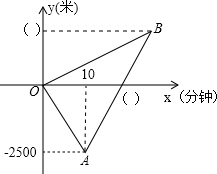早上小芳和妈妈同时从家里出发，小芳步行上学、妈妈骑自行车上班，两人的行进方向正好相反，规定从家往学校的方向为正，如图是她们离家的距离y（米）与时间x（分钟）之间的函数图象，妈妈骑车走了10分钟时接到小芳的电话，立即以原速度前往学校，若已知小芳步行的速度为50米/分钟，并且妈妈与小芳同时到达学校．