题目内容
4.已知一次函数y=(2t-1)x+(t+3)(t是常数).(1)若此函数的图象经过原点,求这个函数的解析式;
(2)若此函数的图象不经过第一象限,求t的取值范围;
(3)求出t=-1时,此函数的图象与两坐标轴围成的三角形的面积.
分析 (1)由已知条件得到t+3=0,于是得到结论;
(2)根据此函数的图象不经过第一象限,得到$\left\{\begin{array}{l}{2t-1<0}\\{t+3<0}\end{array}\right.$,解不等式组即可得到结论;
(3)根据三角形的面积公式即可得到结论.
解答 解:(1)∵此函数的图象经过原点,
∴t+3=0,
∴t=-3,
∴这个函数的解析式为:y=-7x;
(2)∵此函数的图象不经过第一象限,
∴$\left\{\begin{array}{l}{2t-1<0}\\{t+3<0}\end{array}\right.$,
解得t<-3;
(3)∵t=-1,
∴一次函数函数的解析式为:y=-3x+2,
当x=0时,y=2,
当y=0时,x=$\frac{2}{3}$,
∴此函数的图象与两坐标轴的交点分别为(0,2),($\frac{2}{3}$,0),
∴此函数的图象与两坐标轴围成的三角形的面积=$\frac{1}{2}×\frac{2}{3}$×2=$\frac{2}{3}$.
点评 本题考查待定系数法求函数解析式,三角形面积的计算,难度不大,关键是要掌握待定系数法的运用.

练习册系列答案
相关题目
3. 如图是下面某个几何体的三种视图,则该几何体是( )
如图是下面某个几何体的三种视图,则该几何体是( )
 如图是下面某个几何体的三种视图,则该几何体是( )
如图是下面某个几何体的三种视图,则该几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 三棱锥 | D. | 三棱柱 |
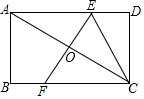 如图,在矩形ABCD中,AB=3,∠BCA=30°,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长为2$\sqrt{3}$.
如图,在矩形ABCD中,AB=3,∠BCA=30°,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长为2$\sqrt{3}$.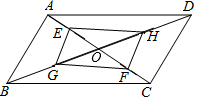 如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AE=CF,BG=DH.求证:GF=HE.
如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AE=CF,BG=DH.求证:GF=HE.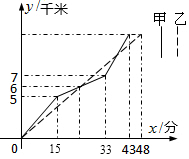 如图表示甲、乙两名同学在”五.一环遗爱湖自行车骑行”比赛中路程y(千米)随时间x(分)变化的图象(全程),根据图象回答下列问题.
如图表示甲、乙两名同学在”五.一环遗爱湖自行车骑行”比赛中路程y(千米)随时间x(分)变化的图象(全程),根据图象回答下列问题.