题目内容
9.对称轴为x=$\frac{7}{2}$的抛物线经过点.A(6,0)和B(0,-4),求抛物线的解析式.分析 设二次函数的解析式式y=a(x-$\frac{7}{2}$)2+h,把A(6,0)和B(0,-4)代入得出方程组,求出方程组的解即可.
解答 解:∵抛物线的对称轴为x=$\frac{7}{2}$,
∴设抛物线的解析式为:y=a(x-$\frac{7}{2}$)2+h,
将A(6,0)和B(0,-4)代入得:$\left\{\begin{array}{l}{\frac{25}{4}a+h=0}\\{\frac{49}{4}a+h=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{h=\frac{25}{6}}\end{array}\right.$
故抛物线线的解析式为:y=-$\frac{2}{3}$(x-$\frac{7}{2}$)2+$\frac{25}{6}$.
点评 本题考查了用待定系数法求二次函数的解析式的应用,根据题意设出合适的二次函数解析式是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
17.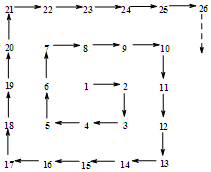 将1开始的自然数,按如图规律排列,在2、3、5、7、10、13、17、…处分别拐第1、2、3、4、5、6、7、…次弯,则第33次弯出的那一个数是( )
将1开始的自然数,按如图规律排列,在2、3、5、7、10、13、17、…处分别拐第1、2、3、4、5、6、7、…次弯,则第33次弯出的那一个数是( )
 将1开始的自然数,按如图规律排列,在2、3、5、7、10、13、17、…处分别拐第1、2、3、4、5、6、7、…次弯,则第33次弯出的那一个数是( )
将1开始的自然数,按如图规律排列,在2、3、5、7、10、13、17、…处分别拐第1、2、3、4、5、6、7、…次弯,则第33次弯出的那一个数是( )| A. | 290 | B. | 226 | C. | 272 | D. | 302 |
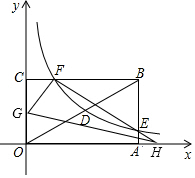 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E,且cos∠BOA=$\frac{4}{5}$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E,且cos∠BOA=$\frac{4}{5}$.
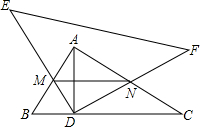 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC边上的高,以D为直角顶点的Rt△DEF绕点旋转,在旋转过程中,DE、EF分别与边AB、AC交于点M、N,则线段MN的最大值与最小值的差为$\frac{16}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC边上的高,以D为直角顶点的Rt△DEF绕点旋转,在旋转过程中,DE、EF分别与边AB、AC交于点M、N,则线段MN的最大值与最小值的差为$\frac{16}{5}$.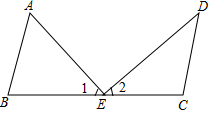 如图,已知AB∥CD,E是BC上一点,∠1=∠A,∠2=∠D,求证:AE⊥DE.
如图,已知AB∥CD,E是BC上一点,∠1=∠A,∠2=∠D,求证:AE⊥DE.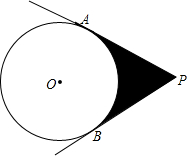 如图,过⊙O外一点P向⊙O作两条切线,切点分别为A,B,若⊙O半径为2,∠APB=60°,则图中阴影部分的面积为4$\sqrt{3}$-$\frac{4}{3}$π.
如图,过⊙O外一点P向⊙O作两条切线,切点分别为A,B,若⊙O半径为2,∠APB=60°,则图中阴影部分的面积为4$\sqrt{3}$-$\frac{4}{3}$π.