题目内容
1.先化简,再求值:$\frac{a-b}{a+3b}$÷$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+6ab+9{b}^{2}}$-1;其中a是8的负的平方根,b是18的算术平方根.分析 首先把所求的分式分子、分母分解因式,把除法转化为乘法,然后进行约分,再通分、进行分式的加减运算即可化简,然后求得a、b的值,代入化简后的式子求解.
解答 解:原式=$\frac{a-b}{a+3b}$•$\frac{(a+3b)^{2}}{(a+b)(a-b)}$-1
=$\frac{a+3b}{a+b}$-1
=$\frac{a+3b-(a+b)}{a+b}$
=$\frac{2b}{a+b}$.
∵a是8的负的平方根,b是18的算术平方根
∴a=-$\sqrt{8}$=-2$\sqrt{2}$,b=$\sqrt{18}$=3$\sqrt{2}$.
∴原式=$\frac{6\sqrt{2}}{-2\sqrt{2}+3\sqrt{2}}$=6.
点评 本题考查了分式的化简求值,正确对所求的式子进行通分、约分是关键.

练习册系列答案
相关题目
11.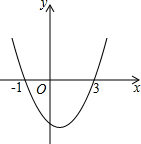 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )
 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a+2b+c<0;④8a+c>0.其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
13.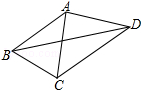 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )| A. | 68° | B. | 88° | C. | 90° | D. | 112° |
8.随着科技技术的不断发展,网上购物越来越便捷,它已成为人们生活的一部分,去年双十一,淘宝天猫的销售额就高达912.17亿元用科学记数法表示为( )
| A. | 9.1217×1010 | B. | 9.1217×109 | C. | 0.91217×103 | D. | 0.91217×102 |
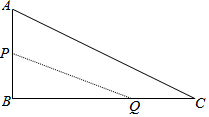 如图,在△ABC中,∠B=90°,AB=6mm,BC=12mm,动点P从点A开始沿边AB向点B以1mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向点C以2mm/s的速度移动(不与点C重合),如果P,Q分别从A,B同时出发,那么经过3秒,四边形APQC的面积最小.
如图,在△ABC中,∠B=90°,AB=6mm,BC=12mm,动点P从点A开始沿边AB向点B以1mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向点C以2mm/s的速度移动(不与点C重合),如果P,Q分别从A,B同时出发,那么经过3秒,四边形APQC的面积最小.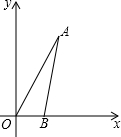 如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6. 将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.
如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6. 将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.