题目内容
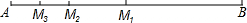 如图,在线段AB上取中点M1,在线段AM1上取中点M2,在线段AM2上取中点M3,依次取中点下去,得到线段AMn,则AM2=
如图,在线段AB上取中点M1,在线段AM1上取中点M2,在线段AM2上取中点M3,依次取中点下去,得到线段AMn,则AM2=考点:两点间的距离
专题:
分析:先根据M1是线段AB的中点用AB表示出AM1的长,同理,用AB表示出AM2的长,找出规律即可得出AMn的长.
解答:解:∵M1是线段AB的中点,
∴AM1=
AB;
∵M2是线段AM1的中点
∴AM2=
AB,
同理,AM3=
AB,
…,
∴AMn=
AB.
故答案为:
,
.
∴AM1=
| 1 |
| 2 |
∵M2是线段AM1的中点
∴AM2=
| 1 |
| 4 |
同理,AM3=
| 1 |
| 8 |
…,
∴AMn=
| 1 |
| 2n |
故答案为:
| 1 |
| 4 |
| 1 |
| 2n |
点评:本题考查的是考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法中,正确的是( )
| A、一个锐角的余角比这个角大 |
| B、一个锐角的补角比这个角大 |
| C、一个锐角的余角比这个角小 |
| D、一个钝角的补角比这个角大 |
 如图,已知AD平分∠BAE,若∠BAD=62°,则∠CAE的度数是( )
如图,已知AD平分∠BAE,若∠BAD=62°,则∠CAE的度数是( )| A、56° | B、55° |
| C、58° | D、62° |
设a,b互为相反数,c,d互为倒数,则2014a+
+2014b的值是( )
| 1 |
| 3cd |
| A、0 | ||
B、
| ||
C、-
| ||
| D、2014 |
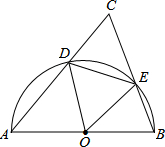 如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC、BC于点D、E.
如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC、BC于点D、E. 已知:如图,点P是△ABC的重心,过P作AC的平行线,分别交AB,BC于点D,E,作DF∥EC,交AC于点F,若△ABC的面积为18cm2,求四边形ECFD的面积.
已知:如图,点P是△ABC的重心,过P作AC的平行线,分别交AB,BC于点D,E,作DF∥EC,交AC于点F,若△ABC的面积为18cm2,求四边形ECFD的面积. 如图,∠1=∠E,∠2与∠C互余,DB⊥AC于点F.试确定图中互相平行的直线,并说明理由.
如图,∠1=∠E,∠2与∠C互余,DB⊥AC于点F.试确定图中互相平行的直线,并说明理由.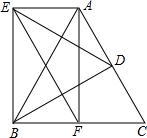 如图,在等边△ABC中,点D是AC的中点,F是BC的中点,以BD为边作等边△BDE.求证:AB=EF,且四边形AEBF是矩形.
如图,在等边△ABC中,点D是AC的中点,F是BC的中点,以BD为边作等边△BDE.求证:AB=EF,且四边形AEBF是矩形.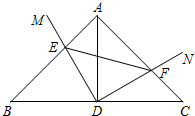 如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.
如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.