题目内容
 已知:如图,点P是△ABC的重心,过P作AC的平行线,分别交AB,BC于点D,E,作DF∥EC,交AC于点F,若△ABC的面积为18cm2,求四边形ECFD的面积.
已知:如图,点P是△ABC的重心,过P作AC的平行线,分别交AB,BC于点D,E,作DF∥EC,交AC于点F,若△ABC的面积为18cm2,求四边形ECFD的面积.考点:三角形的重心
专题:
分析:连接BP并延长交AC于G.由重心的性质得,BP:PG=2:1.由DE∥AC,根据平行线分线段成比例定理可得BD:DA=BP:PG=2:1,于是BD:BA=2:3,AD:AB=1:3.再由DE∥AC,DF∥BC,得出△BDE∽△BAC,△ADF∽△ABC,根据相似三角形的性质得出S△BDE:S△BAC=4:9,S△ADF:S△ABC=1:9,求出
S△BDE=
×S△BAC=8cm2,S△ADF=
×S△BAC=2cm2,进而求出四边形ECFD的面积.
S△BDE=
| 4 |
| 9 |
| 1 |
| 9 |
解答: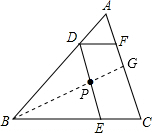 解:连接BP并延长交AC于G.由重心的性质得,BP:PG=2:1.
解:连接BP并延长交AC于G.由重心的性质得,BP:PG=2:1.
∵DE∥AC,
∴BD:DA=BP:PG=2:1,
∴BD:BA=2:3,AD:AB=1:3.
∵DE∥AC,DF∥BC,
∴△BDE∽△BAC,△ADF∽△ABC,
∴S△BDE:S△BAC=4:9,S△ADF:S△ABC=1:9,
∴S△BDE=
×S△BAC=8cm2,S△ADF=
×S△BAC=2cm2,
∴四边形ECFD的面积=18-8-2=8(cm2).
 解:连接BP并延长交AC于G.由重心的性质得,BP:PG=2:1.
解:连接BP并延长交AC于G.由重心的性质得,BP:PG=2:1.∵DE∥AC,
∴BD:DA=BP:PG=2:1,
∴BD:BA=2:3,AD:AB=1:3.
∵DE∥AC,DF∥BC,
∴△BDE∽△BAC,△ADF∽△ABC,
∴S△BDE:S△BAC=4:9,S△ADF:S△ABC=1:9,
∴S△BDE=
| 4 |
| 9 |
| 1 |
| 9 |
∴四边形ECFD的面积=18-8-2=8(cm2).
点评:本题考查了三角形重心的性质,平行线分线段成比例定理,相似三角形的判定与性质,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
若关于的x的分式方程
-1=
有增根,则k可能是( )
| x+1 |
| x-1 |
| k |
| x2-1 |
| A、-1 | B、1 | C、0 | D、2 |
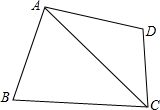 如图,四边形ABCD中AD=AB,∠DAB+∠BCD=180°,求证:CA平分∠DCB.
如图,四边形ABCD中AD=AB,∠DAB+∠BCD=180°,求证:CA平分∠DCB. 如图,∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线.
如图,∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线.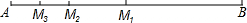 如图,在线段AB上取中点M1,在线段AM1上取中点M2,在线段AM2上取中点M3,依次取中点下去,得到线段AMn,则AM2=
如图,在线段AB上取中点M1,在线段AM1上取中点M2,在线段AM2上取中点M3,依次取中点下去,得到线段AMn,则AM2=