题目内容
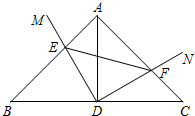 如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.
如图,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.(1)求证:△ADE≌△CDF;
(2)求四边形AEDF的面积;
(3)连结EF.
①当点F在AC边上时总有BE
②若BE=2,求EF的长.
考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)易证AD=DC,∠ADE=∠CDF,即可证明△ADE≌△CDF,即可解题;
(2)根据(1)中结论可得四边形AEDF的面积=S△ADC=
S△ABC,即可解题;
(3)①易证BE=AF,即可求得AF<EF,即可解题;
②根据BE的长即可求得AE,AF的长,即可求得EF的长,即可解题.
(2)根据(1)中结论可得四边形AEDF的面积=S△ADC=
| 1 |
| 2 |
(3)①易证BE=AF,即可求得AF<EF,即可解题;
②根据BE的长即可求得AE,AF的长,即可求得EF的长,即可解题.
解答:(1)证明:∵∠BAC=90°,AB=AC,D为BC中点,
∴∠B=∠C=∠BAD=∠CAD=45°,∠ADC=90°,
∴AD=DC=BD,
∵∠ADE+∠ADF=90°,∠ADF+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(ASA);
(2)解:∵△ADE≌△CDF,
∴四边形AEDF的面积=S△ADC=
S△ABC,
∵S△ABC=
AB•AC=
,
∴四边形AEDF的面积=
;
(3)解:①∵△ADE≌△CDF,
∴AE=CF,
∵AB=AC,
∴BE=AF,
∵FA⊥EA,
∴AF<EF,即BE<EF;
②∵AB=AC=3,BE=2,
∴AE=1,AF=BE=2,
∴EF=
=
.
∴∠B=∠C=∠BAD=∠CAD=45°,∠ADC=90°,
∴AD=DC=BD,
∵∠ADE+∠ADF=90°,∠ADF+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
|
∴△ADE≌△CDF(ASA);
(2)解:∵△ADE≌△CDF,
∴四边形AEDF的面积=S△ADC=
| 1 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
| 9 |
| 2 |
∴四边形AEDF的面积=
| 9 |
| 4 |
(3)解:①∵△ADE≌△CDF,
∴AE=CF,
∵AB=AC,
∴BE=AF,
∵FA⊥EA,
∴AF<EF,即BE<EF;
②∵AB=AC=3,BE=2,
∴AE=1,AF=BE=2,
∴EF=
| AE2+AF2 |
| 5 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
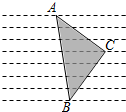 如图,在△ABC中,∠ACB=90°,AC=BC,顶点A、B、C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是2个单位长度,则△ABC的面积是( )
如图,在△ABC中,∠ACB=90°,AC=BC,顶点A、B、C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是2个单位长度,则△ABC的面积是( )| A、24 | B、48 | C、50 | D、100 |
如果一个多项式的次数是5,那么这个多项式的任何一项的次数满足( )
| A、都小于5 | B、都大于5 |
| C、都不小于5 | D、都不大于5 |
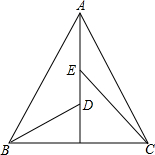 △ABC是等边三角形,∠ADB=120°,∠AEC=120°,求证:CE=BD+ED.
△ABC是等边三角形,∠ADB=120°,∠AEC=120°,求证:CE=BD+ED.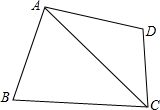 如图,四边形ABCD中AD=AB,∠DAB+∠BCD=180°,求证:CA平分∠DCB.
如图,四边形ABCD中AD=AB,∠DAB+∠BCD=180°,求证:CA平分∠DCB. 如图,在线段AB上取中点M1,在线段AM1上取中点M2,在线段AM2上取中点M3,依次取中点下去,得到线段AMn,则AM2=
如图,在线段AB上取中点M1,在线段AM1上取中点M2,在线段AM2上取中点M3,依次取中点下去,得到线段AMn,则AM2= 如图所示,已知△ABC内接于⊙O,过点A作直线EF切于⊙O,若∠B=50°,求∠CAE的度数.
如图所示,已知△ABC内接于⊙O,过点A作直线EF切于⊙O,若∠B=50°,求∠CAE的度数.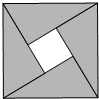 如图是我国古代数学家赵爽的“勾股方圆图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是12,小正方形的面积是2,直角三角形的两直角边分别是a和b,求(a+b)2的值.
如图是我国古代数学家赵爽的“勾股方圆图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是12,小正方形的面积是2,直角三角形的两直角边分别是a和b,求(a+b)2的值.