题目内容
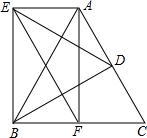 如图,在等边△ABC中,点D是AC的中点,F是BC的中点,以BD为边作等边△BDE.求证:AB=EF,且四边形AEBF是矩形.
如图,在等边△ABC中,点D是AC的中点,F是BC的中点,以BD为边作等边△BDE.求证:AB=EF,且四边形AEBF是矩形.考点:矩形的判定
专题:证明题
分析:根据等边三角形的性质可得AF=BD=BE,再求出∠EBF=∠AFB=90°,然后利用“边角边”证明△ABF和△EFB全等,根据全等三角形对应边相等可得AB=EF,再求出四边形AEBF是平行四边形,然后根据对角线相等的平行四边形是矩形证明即可.
解答:证明:∵等边△ABC中,点D是AC的中点,F是BC的中点,
∴AF=BD,∠CBD=30°,
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴AF=BD=BE,∠EBF=∠AFB=90°,
在△ABF和△EFB中,
,
∴△ABF≌△EFB(SAS),
∴AB=EF,
∵∠AFB=∠EBF=90°,
∴AF∥BE,
又∵∠AF=BE,
∴四边形AEBF是平行四边形,
∵AB=EF,
∴四边形AEBF是矩形,
故AB=EF,且四边形AEBF是矩形.
∴AF=BD,∠CBD=30°,
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴AF=BD=BE,∠EBF=∠AFB=90°,
在△ABF和△EFB中,
|
∴△ABF≌△EFB(SAS),
∴AB=EF,
∵∠AFB=∠EBF=90°,
∴AF∥BE,
又∵∠AF=BE,
∴四边形AEBF是平行四边形,
∵AB=EF,
∴四边形AEBF是矩形,
故AB=EF,且四边形AEBF是矩形.
点评:本题考查了矩形的判定,等边三角形的性质,全等三角形的判定与性质,平行四边形的判定与性质,熟记各性质并确定出全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个数的立方根等于-2,则这个数的相反数是( )
| A、8 | B、-8 | C、4 | D、-4 |
 如图,该图是一个正方体的展开图,把展开图折叠成正方体后,有“少”字一面的相对面上的字是( )
如图,该图是一个正方体的展开图,把展开图折叠成正方体后,有“少”字一面的相对面上的字是( )| A、强 | B、中 | C、国 | D、梦 |
 如图,∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线.
如图,∠AMB=90°,∠CMD=90°,ME、MF分别是射线MA、MD的反向延长线. 已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
已知△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.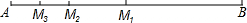 如图,在线段AB上取中点M1,在线段AM1上取中点M2,在线段AM2上取中点M3,依次取中点下去,得到线段AMn,则AM2=
如图,在线段AB上取中点M1,在线段AM1上取中点M2,在线段AM2上取中点M3,依次取中点下去,得到线段AMn,则AM2=
 如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠EOF的度数.
如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOE=4:1,求∠EOF的度数.