题目内容
6. 如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时:
如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时:(1)求证:∠CPO=∠CDO;
(2)求证:CP=CD;
(3)下列两个结论:①AD-BP的值不变;②AD+BP的值不变,选择正确的结论求其值.
分析 (1)根据三角形内角和定理得出∠CPO+∠OKP=∠CDO+∠CKD=90°,根据∠OKP=∠CKD即可求出∠CPO=∠CDO;
(2)过C作CN⊥x轴于N,CQ⊥y轴于Q,则∠CND=∠CQP=90°,求出CQ=CN,根据AAS推出△CND≌△CQP即可;
(3)求出AN=3,BQ=5,根据全等得QP=ND,求出AD+BP=AN+QB,代入求出即可.
解答 (1)证明:∵x轴⊥y轴,CP⊥CD,
∴∠DCP=∠DOP=90°,
∴∠CPO+∠OKP=∠CDO+∠CKD=90°,
∵∠OKP=∠CKD,
∴∠CPO=∠CDO;
(2)证明:过C作CN⊥x轴于N,CQ⊥y轴于Q,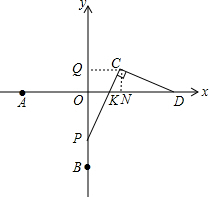
则∠CND=∠CQP=90°,
∵C(1,1),
∴CQ=CN,
在△CND和△CQP中,
$\left\{\begin{array}{l}{∠CDN=∠CPQ}\\{∠CQP=∠CND}\\{CN=CQ}\end{array}\right.$,
∴△CND≌△CQP(AAS),
∴CP=CD;
(3)解:AD+BP的值不变,
∵A(-2,0),B(0,-4),C(1,1),
∴AN=2+1=3,BQ=4+1=5,
∵△CND≌△CQP,
∴QP=ND,
∵AD+BP=AN+ND+BP=AN+QP+BP=AN+QB=3+5=8,
∴AD+BP的值不变,是8.
点评 本题考查了坐标与图形的性质,全等三角形的性质和判定的应用,能正确作出辅助线并求出△CND≌△CQP是解此题的关键.

练习册系列答案
相关题目
 如图,小刚、小明一起去精品文具店买同种钢笔和同种练习本.下面是小刚、小明与售货员的对话:
如图,小刚、小明一起去精品文具店买同种钢笔和同种练习本.下面是小刚、小明与售货员的对话: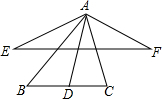 如图,在△ABC中,AD为BC边上的中线,若∠BAC<90°,作EA⊥AC,FA⊥BA,且AE=AC,AF=AB.连接EF,写出AD与EF的数量关系,并证明.
如图,在△ABC中,AD为BC边上的中线,若∠BAC<90°,作EA⊥AC,FA⊥BA,且AE=AC,AF=AB.连接EF,写出AD与EF的数量关系,并证明. 已知,如图,AB∥CD,AD交BC于点O,EF过点O,分别交AB,CD于点E,F,且AE=DF.求证:O是EF的中点.
已知,如图,AB∥CD,AD交BC于点O,EF过点O,分别交AB,CD于点E,F,且AE=DF.求证:O是EF的中点. 如图,四边形OACB中,CM⊥OA,∠A+∠B=180°,OA+OB=2OM,CA=CB.求证:OC平分∠AOB.
如图,四边形OACB中,CM⊥OA,∠A+∠B=180°,OA+OB=2OM,CA=CB.求证:OC平分∠AOB. 如图所示,AB=AC,点D,E分别在AC,AB上,AF⊥CE,AG⊥BD,垂足分别为F,G,AF=AG,下列结论:①∠B=∠C;②∠EAF=∠DAG;③AD=AE;④BE=CD
如图所示,AB=AC,点D,E分别在AC,AB上,AF⊥CE,AG⊥BD,垂足分别为F,G,AF=AG,下列结论:①∠B=∠C;②∠EAF=∠DAG;③AD=AE;④BE=CD