题目内容
定义:若抛物线y=ax2+bx+c与x轴的两个交点和顶点构成直角三角形,则称这条抛物线为“直角抛物线”.
(1)抛物线y=x2-1 直角抛物线(填“是”或“不是”);
(2)直角抛物线y=a(x+2)2-3与x轴交于点A、B(A在B的左侧),顶点为P,求a的值.
(1)抛物线y=x2-1
(2)直角抛物线y=a(x+2)2-3与x轴交于点A、B(A在B的左侧),顶点为P,求a的值.
考点:二次函数图象上点的坐标特征,等腰直角三角形
专题:
分析:(1)先求得与x轴的两交点坐标为(-1,0)和(1,0),顶点坐标(0,-1),利用勾股定理可判定;
(2)由题意可知△PAB为等腰直角三角形,设对称轴与x轴的交点为F,则有AF=BF=PF,根据顶点坐标可求得B点坐标,代入可求得a.
(2)由题意可知△PAB为等腰直角三角形,设对称轴与x轴的交点为F,则有AF=BF=PF,根据顶点坐标可求得B点坐标,代入可求得a.
解答:解:
(1)令y=0可得x2-1=0,解得x=±1,
∴与x轴的交点坐标为C(-1,0)和D(1,0),
又顶点E坐标为(0,-1),
∴OE=OC=OD,
∴∠CED=90°,
∴抛物线y=x2-1是直角抛物线,
故答案为:是;
(2)设对称轴与x轴的交点为F,
∵y=a(x+2)2-3是直角抛物线,顶点坐标为P(-2,-3),
∴AF=BF=PF=3,且OF=2,
∴OB=BF-OF=3-2=1,
∴B为(1,0),代入抛物线解析式可得0=a(1+2)2-3,
解得a=
.
(1)令y=0可得x2-1=0,解得x=±1,
∴与x轴的交点坐标为C(-1,0)和D(1,0),
又顶点E坐标为(0,-1),
∴OE=OC=OD,
∴∠CED=90°,
∴抛物线y=x2-1是直角抛物线,
故答案为:是;
(2)设对称轴与x轴的交点为F,
∵y=a(x+2)2-3是直角抛物线,顶点坐标为P(-2,-3),
∴AF=BF=PF=3,且OF=2,
∴OB=BF-OF=3-2=1,
∴B为(1,0),代入抛物线解析式可得0=a(1+2)2-3,
解得a=
| 1 |
| 3 |
点评:本题主要考查二次函数与x轴的交点,利用二次函数的对称性得到△PAB为等腰直角三角形是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y=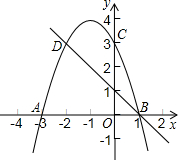 如图,二次函数y2=ax2+bx+3的图象与x轴相交于点A(-3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y1=mx+n的图象经过B、D两点.
如图,二次函数y2=ax2+bx+3的图象与x轴相交于点A(-3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y1=mx+n的图象经过B、D两点. 有一个数值转换器,原理如图所示,若开始输入x的值是7,可发现第一次输出的结果是10,第二次输出的结果是5,…,请你探索第2014次输出的结果是
有一个数值转换器,原理如图所示,若开始输入x的值是7,可发现第一次输出的结果是10,第二次输出的结果是5,…,请你探索第2014次输出的结果是 如图,在长度为1个单位长度的正方形网格中,点A、B、C在小正方形的顶点上.
如图,在长度为1个单位长度的正方形网格中,点A、B、C在小正方形的顶点上.