题目内容
3. 如图,等腰梯形ABCD中,AB∥DC,BD平分∠ABC,∠DAB=60°,若梯形周长为8cm,则AD=$\frac{8}{5}$cm.
如图,等腰梯形ABCD中,AB∥DC,BD平分∠ABC,∠DAB=60°,若梯形周长为8cm,则AD=$\frac{8}{5}$cm.
分析 由梯形ABCD是等腰梯形,于是得到AD=BC,∠DAB=∠ABC=60°,由于AB∥DC,得到∠CDB=∠ABD,由BD平分∠ABC,得到∠ABD=∠CBD=30°,于是求得∠CDB=∠CBD,∠ADB=90°,根据直角三角形的性质得到CD=BC,AB=2AD,于是得到结论.
解答 解:∵梯形ABCD是等腰梯形,
∴AD=BC,∠DAB=∠ABC=60°,
∵AB∥DC,
∴∠CDB=∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠CBD=30°,
∴∠CDB=∠CBD,∠ADB=90°,
∴CD=BC,AB=2AD,
∵梯形周长为8cm,
∴AD=$\frac{1}{5}$×8=$\frac{8}{5}$cm.
故答案为:$\frac{8}{5}$cm.
点评 本题考查了等腰梯形的性质,直角三角形的性质,角的平分线的性质,熟练掌握等腰梯形的性质是解题的关键.

练习册系列答案
相关题目
8.2的算术平方根是( )
| A. | $±\sqrt{2}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | ±2 |
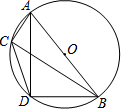 如图,等腰直角三角形△ABD内接于⊙O,AB为直径,点C为劣弧AD上一点,且AC=4,CD=$6\sqrt{2}$,则BC的长为( )
如图,等腰直角三角形△ABD内接于⊙O,AB为直径,点C为劣弧AD上一点,且AC=4,CD=$6\sqrt{2}$,则BC的长为( )