题目内容
 如图,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED的延长线交CA于F.求证:AC•CF=BC•DF.
如图,CD是Rt△ABC斜边AB上的高,E为BC的中点,ED的延长线交CA于F.求证:AC•CF=BC•DF.考点:相似三角形的判定与性质
专题:证明题
分析:先证明△ADC∽△CDB可得
=
,再结合条件证明△FDC∽△FAD,可得
=
,则可证得结论.
| AD |
| CD |
| AC |
| BC |
| DF |
| CF |
| AD |
| DC |
解答:证明:
∵∠ACB=90°,CD⊥AB,
∴∠DAC+∠B=∠B+∠DCB=90°,
∴∠DAC=∠DCB,且∠ACD=∠CDB,
∴△ADC∽△CDB,
∴
=
,
∵E为BC中点,
∴DE=CE,
∴∠EDC=∠DCE=∠DAC,
∴∠FDC=∠FAD,且∠F=∠F,
∴△FDC∽△FAD,
∴
=
,
∴
=
,
∴AC•CF=BC•DF.
∵∠ACB=90°,CD⊥AB,
∴∠DAC+∠B=∠B+∠DCB=90°,
∴∠DAC=∠DCB,且∠ACD=∠CDB,
∴△ADC∽△CDB,
∴
| AD |
| CD |
| AC |
| BC |
∵E为BC中点,
∴DE=CE,
∴∠EDC=∠DCE=∠DAC,
∴∠FDC=∠FAD,且∠F=∠F,
∴△FDC∽△FAD,
∴
| DF |
| CF |
| AD |
| DC |
∴
| AC |
| BC |
| DF |
| CF |
∴AC•CF=BC•DF.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的对应边成比例是解题的关键,注意直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
 如图所示,被遮挡的点的坐标可能是( )
如图所示,被遮挡的点的坐标可能是( )| A、(-2,-3) |
| B、(-2,3) |
| C、(2,-3) |
| D、(2,3) |
 将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是
将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是 一个函数的图象是双曲线(如图),根据图象,求出这个函数的解析式和m的值.
一个函数的图象是双曲线(如图),根据图象,求出这个函数的解析式和m的值.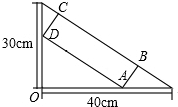 在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.
在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.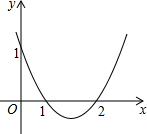 如图,抛物y=x2+bx+c与x轴交于点(1,0)、(2,0),x1、x2是关于x的方程x2+bx+c=0的两个根,则x1+x2=
如图,抛物y=x2+bx+c与x轴交于点(1,0)、(2,0),x1、x2是关于x的方程x2+bx+c=0的两个根,则x1+x2= 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G,求证:AC•DG=AG•DF.
如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G,求证:AC•DG=AG•DF.