题目内容
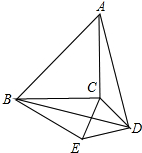
如图，小正方形的边长均为1的正方形网格中，O的圆心在格点上，求∠AED的余弦值．考点：圆周角定理,勾股定理,锐角三角函数的定义
专题：网格型
分析：先在Rt△ACB中利用勾股定理计算出BC=
，再利用余弦的定义计算出cos∠ABC=
=
，然后根据圆周角定理得到∠AED=∠ABC，即有cos∠AED=
．
| 5 |
| AB |
| BC |
2
| ||
| 5 |
2
| ||
| 5 |
解答：解：在Rt△ACB中，∵AC=1，AB=2，
∴BC=
=
，
∴cos∠ABC=
=
=
，
∵∠AED=∠ABC，
∴cos∠AED=
．
∴BC=
| AC2+AB2 |
| 5 |
∴cos∠ABC=
| AB |
| BC |
| 2 | ||
|
2
| ||
| 5 |
∵∠AED=∠ABC，
∴cos∠AED=
2
| ||
| 5 |
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了锐角三角函数的定义．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
如图，以等腰直角三角形ABC的斜边AB为边向内作等边△ABD，连接DC，以DC为边，作等边△DCE，点B、E在CD的同侧．计算
+
的结果为（ ）
| 48 |
| ||
| 2 |
A、5
| ||||
B、
| ||||
C、4
| ||||
D、5
|
下列方程的解为x=3的是（ ）
| A、-3x=2-4x | ||||
B、
| ||||
| C、2（2+x）=1-（3-x） | ||||
| D、2x-1=5 |