题目内容
17.已知代数式:A=$\frac{3}{x+2}$,B=$\frac{x-2}{x+3}÷\frac{{{x^2}-4}}{2x+6}-\frac{5}{x+2}$.(1)试证明:若A、B均有意义,则它们的值互为相反数;
(2)若代数式A、B中的x是满足不等式3(x-3)<6-2x的正整数解,求A-B的值.
分析 (1)根据题意证明A+B=0即可;
(2)先根据分式混合运算的法则求出A-B的式子,再根据求出不等式3(x-3)<6-2x的解集,根据x是满足不等式3(x-3)<6-2x的正整数解求出x的值,代入原式进行计算即可.
解答 (1)证明:∵A=$\frac{3}{x+2}$,B=$\frac{x-2}{x+3}$÷$\frac{{x}^{2}-4}{2x+6}$-$\frac{5}{x+2}$,
∴A+B=$\frac{3}{x+2}$+$\frac{x-2}{x+3}$÷$\frac{{x}^{2}-4}{2x+6}$-$\frac{5}{x+2}$
=$\frac{3}{x+2}$+$\frac{x-2}{x+3}$•$\frac{2(x+3)}{(x+2)(x-2)}$-$\frac{5}{x+2}$
=$\frac{3}{x+2}$+$\frac{2}{x+2}$-$\frac{5}{x+2}$
=$\frac{3+2-5}{x+2}$
=0;
(2)解:∵A=$\frac{3}{x+2}$,B=$\frac{x-2}{x+3}$÷$\frac{{x}^{2}-4}{2x+6}$-$\frac{5}{x+2}$,
∴A-B=$\frac{3}{x+2}$-$\frac{x-2}{x+3}$÷$\frac{{x}^{2}-4}{2x+6}$+$\frac{5}{x+2}$
=$\frac{3}{x+2}$-$\frac{2}{x+2}$+$\frac{5}{x+2}$
=$\frac{6}{x+2}$,
解不等式3(x-3)<6-2x得,x<3.
∵x是满足不等式3(x-3)<6-2x的正整数解,
∴x1=1,x2=2(舍去)
∴当x=1时,原式=$\frac{6}{1+2}$=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

①若a≤0,则|a|=-a;②若ma2>na2,则m>n;③直角三角形斜边上的中线等于斜边的一半;④矩形的两条对角线相等.
其中原命题为真命题,逆命题为假命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | x2+x4=x6 | B. | 2x+3y=5xy | C. | (x3)2=x6 | D. | x6÷x3=x2 |

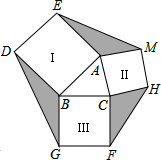 如图,已知△ABC,BC=5,AB=4,分别以AB、BC、CA为边向外作正方形,则图中阴影部分的面积之和的最大值是30.
如图,已知△ABC,BC=5,AB=4,分别以AB、BC、CA为边向外作正方形,则图中阴影部分的面积之和的最大值是30.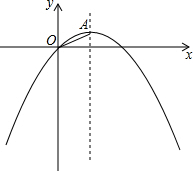 已知:在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A
已知:在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A