题目内容
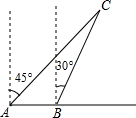 如图所示,一渔船正以每小时30海里的速度由西向东航行,在A处看见小岛C在船的北偏东45°方向上.40min后,渔船行至B处,此时看见小岛C在船的北偏东30°.若以小岛C为中心周围30海里是危险区,问这艘渔船继续向东航行是否有进入危险区的可能?
如图所示,一渔船正以每小时30海里的速度由西向东航行,在A处看见小岛C在船的北偏东45°方向上.40min后,渔船行至B处,此时看见小岛C在船的北偏东30°.若以小岛C为中心周围30海里是危险区,问这艘渔船继续向东航行是否有进入危险区的可能?考点:解直角三角形的应用-方向角问题
专题:
分析:根据题意用未知数表示出BD,CD的长,再利用等腰三角形的性质得出即可.
解答: 解:如图所示:
解:如图所示:
过点C作CD⊥AB于点D,
由题意可得:∠CAD=∠ACD=45°,∠BCD=30°,
则设CD=x海里,故BD=
x海里,
故AD=DC,
∵一渔船正以每小时30海里的速度由西向东航行,40min后,渔船行至B处,
∴AB=
×30=20(海里),
即20+
x=x,
解得:x=30+10
,
∵30+10
>30,
∴这艘渔船继续向东航行没有有进入危险区的可能.
 解:如图所示:
解:如图所示:过点C作CD⊥AB于点D,
由题意可得:∠CAD=∠ACD=45°,∠BCD=30°,
则设CD=x海里,故BD=
| ||
| 3 |
故AD=DC,
∵一渔船正以每小时30海里的速度由西向东航行,40min后,渔船行至B处,
∴AB=
| 40 |
| 60 |
即20+
| ||
| 3 |
解得:x=30+10
| 3 |
∵30+10
| 3 |
∴这艘渔船继续向东航行没有有进入危险区的可能.
点评:此题主要考查了解直角三角形的应用,根据题意得出DC的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
做重复实验同一枚啤酒瓶盖1000次.经过统计得“凸面向 上”的频率0.48,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为( )
| A、0.24 | B、0.48 |
| C、0.50 | D、0.52 |
 如图的图形是由一长方形及一等腰三角形所组成.
如图的图形是由一长方形及一等腰三角形所组成.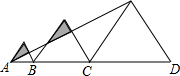 已知三个边长分别为2、3、5的正三角形从左到右如图排列,则图中阴影部分面积为
已知三个边长分别为2、3、5的正三角形从左到右如图排列,则图中阴影部分面积为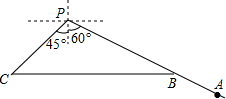 如图,甲船在港口P的南偏西60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向.求乙船的航行速度.(结果精确到个位,参考数据:
如图,甲船在港口P的南偏西60°方向,距港口30海里的A处,沿AP方向以每小时5海里的速度匀速驶向港口P.乙船从港口P出发,沿南偏东45°方向匀速驶离港口P,现两船同时出发,2小时后甲船到达B处,乙船到达C处,此时乙船恰好在甲船的正西方向.求乙船的航行速度.(结果精确到个位,参考数据:
 已知:如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=8cm,CE=6cm,则平行四边形ABCD的周长为
已知:如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=8cm,CE=6cm,则平行四边形ABCD的周长为