题目内容
16.已知三角形的三边分别为3,x,4,那么最长边x的取值范围是4≤x<7.分析 根据三角形的任意两边之和大于第三边,两边之差小于第三边的取值范围,再根据x是最长边求解即可.
解答 解:由三角形的三边关系定理可得:
4-3<x<4+3,
即1<x<7.
又∵x是三角形中最长的边,
∴4≤x<7.
故答案为:4≤x<7.
点评 此题主要考查了三角形的三边关系定理,三角形中第三边的范围是:大于已知的两边的差,而小于已知两边的和.解题时需要注意:x是三角形最长边的条件,这是本题最容易出错的地方.

练习册系列答案
相关题目
4.下列说法正确的是( )
| A. | 零是正数不是负数 | B. | 不是正数的数一定是负数 | ||
| C. | 零既是正数也是负数 | D. | 零既不是正数也不是负数 |
1.某特技飞行队在名胜风景旅游区做特技表演,其中一架飞机起飞后的高度变化如表:
(1)此时这架飞机比起飞点高了多少千米?
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
| 高度变化 | 上升4.5km | 下降3.2km | 上升1.1km | 下降1.4km |
| 记作 | +4.5km | -3.2km | +1.1km | -1.4km |
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
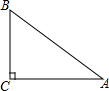 已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是5km.
已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是5km.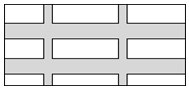 如图,要设计一幅宽20厘米,长30厘米的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:1,如果要使彩条所占面积是图案面积的一半,那么竖彩条宽度是多少?若设竖彩条宽度是x厘米,则根据题意可列方程(30-2x)(20-4x)=300.
如图,要设计一幅宽20厘米,长30厘米的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:1,如果要使彩条所占面积是图案面积的一半,那么竖彩条宽度是多少?若设竖彩条宽度是x厘米,则根据题意可列方程(30-2x)(20-4x)=300. 如图是小强用八块相同的小立方块搭建的一个积木,他从左面看到的形状图是( )
如图是小强用八块相同的小立方块搭建的一个积木,他从左面看到的形状图是( )



