题目内容
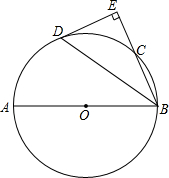 如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC的延长线于点E.
如图,AB是⊙O的直径,∠ABC的平分线BD交⊙O于D,过点D作DE⊥BC的延长线于点E.(1)求证:DE是⊙O的切线;
(2)若AB=10.BD=8,求线段EC的长.
考点:切线的判定
专题:
分析:(1)利用角平分线的定义结合等腰三角形的性质得出∠ODB=∠DBE,进而得出∠ODE=90°,即可得出答案;
(2)首先利用△ABD∽△EBD,则
=
=
,进而得出BE,DE的长,再利用切割线定理得出答案.
(2)首先利用△ABD∽△EBD,则
| AB |
| BD |
| BD |
| BE |
| AD |
| DE |
解答: (1)证明:连接OD,
(1)证明:连接OD,
∵∠ABC的平分线BD交⊙O于D,
∴∠EBD=∠DBA,
∵DO=BO,
∴∠ODB=∠OBD,
∴∠ODB=∠DBE,
∴DO∥BE,
∵∠E=90°,
∴∠ODE=90°,
∴DE是⊙O的切线;
(2)解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠ABD=∠DBE,
∴△ABD∽△EBD,
∴
=
=
,
∵AB=10,BD=8
∴AD=6,
∴
=
=
,
解得:BE=6.4,DE=4.8,
由切割线定理可得:DE2=EC×BE,
解得:EC=3.6.
 (1)证明:连接OD,
(1)证明:连接OD,∵∠ABC的平分线BD交⊙O于D,
∴∠EBD=∠DBA,
∵DO=BO,
∴∠ODB=∠OBD,
∴∠ODB=∠DBE,
∴DO∥BE,
∵∠E=90°,
∴∠ODE=90°,
∴DE是⊙O的切线;
(2)解:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠ABD=∠DBE,
∴△ABD∽△EBD,
∴
| AB |
| BD |
| BD |
| BE |
| AD |
| DE |
∵AB=10,BD=8
∴AD=6,
∴
| 10 |
| 8 |
| 8 |
| BE |
| 6 |
| DE |
解得:BE=6.4,DE=4.8,
由切割线定理可得:DE2=EC×BE,
解得:EC=3.6.
点评:此题主要考查了切线的判定以及相似三角形的判定与性质,得出△ABD∽△EBD是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知∠APC、∠BPD都是直角,∠APD=110°,求∠BPC的度数.
如图,已知∠APC、∠BPD都是直角,∠APD=110°,求∠BPC的度数. 将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是
将一个三角尺和一把直尺如图放置,则∠α+∠β的度数是 如图是平放在桌面上的长方体木块,其长为14cm,宽为10cm,高为20cm,点B是高CD的中点,一只蜘蛛要沿长方体木块的表面从A点爬到B点,请你求出蜘蛛爬行的最短路程是多少?
如图是平放在桌面上的长方体木块,其长为14cm,宽为10cm,高为20cm,点B是高CD的中点,一只蜘蛛要沿长方体木块的表面从A点爬到B点,请你求出蜘蛛爬行的最短路程是多少?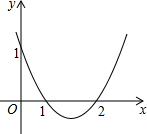 如图,抛物y=x2+bx+c与x轴交于点(1,0)、(2,0),x1、x2是关于x的方程x2+bx+c=0的两个根,则x1+x2=
如图,抛物y=x2+bx+c与x轴交于点(1,0)、(2,0),x1、x2是关于x的方程x2+bx+c=0的两个根,则x1+x2=