题目内容
如图，在矩形ABCD中，tan∠BAC=3，AD=18，求矩形ABCD的面积．考点：解直角三角形
专题：
分析：先根据四边形ABCD是矩形可知AD=BC，∠ABC=90°，再由tan∠BAC=3可设AB=x，则BC=3x，再根据AD=18求出x的值，根据矩形的面积即可得出结论．
解答：解：∵四边形ABCD是矩形，
∴AD=BC=18，∠ABC=90°，
∵tan∠BAC=3，
∴设AB=x，则BC=3x，
∴3x=18，解得x=6，
∴AB=6，BC=18，
∴S矩形ABCD=6×18=108．
∴AD=BC=18，∠ABC=90°，
∵tan∠BAC=3，
∴设AB=x，则BC=3x，
∴3x=18，解得x=6，
∴AB=6，BC=18，
∴S矩形ABCD=6×18=108．
点评：本题考查的是解直角三角形，熟知锐角三角函数的定义及矩形的性质是解答此题的关键．
练习册系列答案
相关题目
-（-
）的相反数是（ ）
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
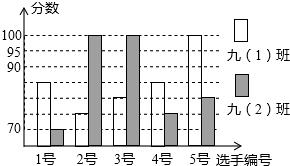某中学开展“我的中国梦”演讲比赛活动，九（1）、九（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如下图所示．
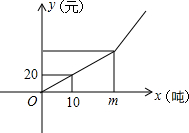某市制定了一套节约用水的管理措施，其中规定每月用水量超过m（吨）时，超过部分每吨加收环境保护费
如图，在△ABC中，AB=AC，BC=20，△ABC的面积为
一条排水管的截面如图所示，已知水面宽AB=10cm，截面圆⊙O的半径OC⊥AB于D，且OD：DC=3：2，求⊙O的直径．
如图，一块三角形铁皮，其中∠B=30°，∠C=45°，AC=12