题目内容
13.五水共治检查组从A市到B市有一天的路程,计划上午比下午多走100千米到C市吃午饭.由于堵车,中午才赶到一个小镇,只行驶了原计划的三分之一,过了小镇,汽车赶了400千米才停下来休息.司机说:“再走从C市到这里路程的二分之一就到达目的地了”.则A市到B市的路程为( )| A. | 600千米 | B. | 700千米 | C. | 800千米 | D. | 1200千米 |
分析 设AB两市相距x千米,根据题目的叙述用x表示出DE的长,即可求得答案.
解答  解:设AB两市相距x千米,
解:设AB两市相距x千米,
则由题可知:CA=$\frac{1}{2}$x+50千米
BC=$\frac{1}{2}$x-50千米
∴BE=$\frac{1}{3}$BC=$\frac{1}{6}$x-$\frac{50}{3}$km
CE=$\frac{2}{3}$BC=$\frac{1}{3}$x-$\frac{100}{3}$km
AD=$\frac{1}{3}$AC=$\frac{1}{3}$($\frac{1}{2}$x+50)=$\frac{1}{6}$x+$\frac{50}{3}$DE=AB-AD-BE=x-($\frac{1}{6}$x+$\frac{50}{3}$)-($\frac{1}{6}$x-$\frac{50}{3}$)=$\frac{2}{3}$x,
∵DE=400,
∴400=$\frac{2}{3}$x,
∴x=600(km)
∴AB两地相距600千米;
故选A.
点评 此题考查了一元一次方程的应用,本题的难度较大,能够正确利用x表示出DE的长度是解题关键.

练习册系列答案
相关题目
3.一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动.设该机器人每秒前进或后退1步,并且每步的距离是一个单位长度,xn表示第n秒时机器人在数轴上的位罝所对应的数.给出下列结论:
①x3=3;②x5=1;③x108<x104;④x2007<x2008,其中,正确结论的序号是( )
①x3=3;②x5=1;③x108<x104;④x2007<x2008,其中,正确结论的序号是( )
| A. | ①③ | B. | ②③ | C. | ①②③ | D. | ①②④ |
1.据某市旅游局统计,今年“五一”小长假期间,各旅游景点门票收入约3700万元,数据“3700万”用科学记数法表示为( )
| A. | 3.7×107 | B. | 3.7×108 | C. | 0.37×108 | D. | 37×108 |
8.-2016的倒数是( )
| A. | 2016 | B. | 2016 | C. | $\frac{1}{2016}$ | D. | $-\frac{1}{2016}$ |
18.下列图形都是由正方形按一定规律组成的,其中第①个图形中一共有8个正方形,第②个图形中一共有15个正方形,第③个图形中一共有22个正方形,…,按此规律排列,则第⑥个图形中正方形的个数为( )


| A. | 50 | B. | 48 | C. | 43 | D. | 40 |
5.与无理数$\sqrt{35}$最接近的整数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
2.方程1-$\frac{x+3}{6}$=$\frac{x}{2}$的解为( )
| A. | x=-$\frac{1}{2}$ | B. | x=$\frac{3}{4}$ | C. | x=$\frac{9}{4}$ | D. | x=1 |
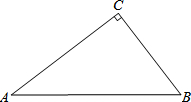 如图,△ABC中,∠A+∠B=90°.
如图,△ABC中,∠A+∠B=90°.