题目内容
操作发现
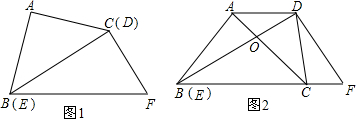
将一副直角三角板如图(1)摆放,能够发现等腰直角三角板ABC的斜边BC与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图1中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上.AC与BD交于点O,连接CD,如图2.
(1)若DF=4,求BF的长;
(2)求证:△CDO是等腰三角形.
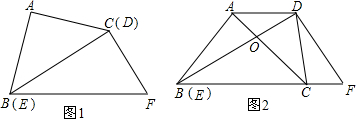
将一副直角三角板如图(1)摆放,能够发现等腰直角三角板ABC的斜边BC与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图1中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上.AC与BD交于点O,连接CD,如图2.
(1)若DF=4,求BF的长;
(2)求证:△CDO是等腰三角形.
考点:等腰三角形的判定,含30度角的直角三角形,等腰直角三角形
专题:
分析:(1)根据30°角所对直角边是斜边一半的性质即可求得BF的长,即可解题;
(2)根据BC=DE和∠DEF=30°可求得∠BDC和∠BCD的值,根据∠ACB=45°即可求得∠DOC的值,即可解题.
(2)根据BC=DE和∠DEF=30°可求得∠BDC和∠BCD的值,根据∠ACB=45°即可求得∠DOC的值,即可解题.
解答:解:(1)∵在Rt△DEF中,∠DEF=30°,∠EDF=90°,DF=4,
∴BF=8.
(2)∵在△BDC 中,BC=DE,
∴∠BDC=∠BCD.
∵∠DEF=30°,
∴∠BDC=∠BCD=75°,
∵∠ACB=45°,
∴∠DOC=30°+45°=75°.
∴∠DOC=∠BDC,
∴△CDO是等腰三角形.
∴BF=8.
(2)∵在△BDC 中,BC=DE,
∴∠BDC=∠BCD.
∵∠DEF=30°,
∴∠BDC=∠BCD=75°,
∵∠ACB=45°,
∴∠DOC=30°+45°=75°.
∴∠DOC=∠BDC,
∴△CDO是等腰三角形.
点评:本题考查了等腰三角形的判定,考查了30°角所对直角边是斜边一半的性质,本题中求证∠DOC=∠BDC是解题的关键.

练习册系列答案
相关题目
若单项式-
的系数为m,次数为n,则m+n=( )
| 3xy2 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
| D、4 |
 如图,圆的半径是5
如图,圆的半径是5 如图,△ABC的面积为63,D是BC上的一点,且BD:CD=1:2,DE∥AB交AC于点E,延长DE到F,使FE:ED=2:1,连接BF,则△BDF的面积为 ( )
如图,△ABC的面积为63,D是BC上的一点,且BD:CD=1:2,DE∥AB交AC于点E,延长DE到F,使FE:ED=2:1,连接BF,则△BDF的面积为 ( )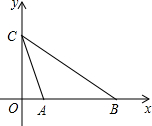 如图,平面直角坐标系中,A、B在x轴上,A(2,0)、B(8,0),点C为y轴上一动点,当∠ACB最大时,C点坐标为
如图,平面直角坐标系中,A、B在x轴上,A(2,0)、B(8,0),点C为y轴上一动点,当∠ACB最大时,C点坐标为 如图,抛物线y=-x2+2(m+1)x+m+3与x轴交于A,B两点,且OA:OB=1:3,求m的值.
如图,抛物线y=-x2+2(m+1)x+m+3与x轴交于A,B两点,且OA:OB=1:3,求m的值.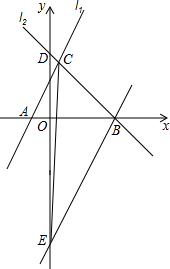 如图,直线l1,l2,交于C点,直线l1与x轴交于A,直线l2与x轴交于B(3,0),与y轴交于D(0,3),已知直线l1的函数解析式为y=2x+2.
如图,直线l1,l2,交于C点,直线l1与x轴交于A,直线l2与x轴交于B(3,0),与y轴交于D(0,3),已知直线l1的函数解析式为y=2x+2.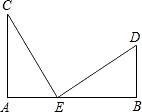 已知,如图,AC⊥AB,DB⊥AB,AC=BE,AE=BD,
已知,如图,AC⊥AB,DB⊥AB,AC=BE,AE=BD,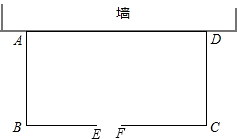 哈市某养鸡专业户要围成一个矩形鸡舍,鸡舍的一边利用足够长的墙,另三边用总长为31米的篱笆恰好围成,围成的鸡舍是如图所示的矩形ABCD,在BC上留有1米宽的门EF(门不用篱笆).设AB边的长为x米,矩形ABCD的面积为S平方米.
哈市某养鸡专业户要围成一个矩形鸡舍,鸡舍的一边利用足够长的墙,另三边用总长为31米的篱笆恰好围成,围成的鸡舍是如图所示的矩形ABCD,在BC上留有1米宽的门EF(门不用篱笆).设AB边的长为x米,矩形ABCD的面积为S平方米.