题目内容
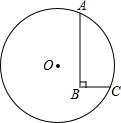 如图,圆的半径是5
如图,圆的半径是5| 2 |
考点:垂径定理,勾股定理
专题:计算题
分析:延长AB、CB分别交⊙O于E、D,作OM⊥AB于M,ON⊥CD于N,连结OB、OA、OD,如图,设OM=a,ON=b,先证明四边形OMBN为矩形得到OM=BN=a,ON=BM=b,再根据垂径定理,由ON⊥CD得到DN=CN=a+2,在△AOM中利用勾股定理得(6-b)2+a2=(5
)2①,在Rt△OND中根据勾股定理得(a+2)2+b2=(5
)2②,然后解由①②所组成的方程组得到当b=1时,a=5,最后在Rt△OBM中根据勾股定理计算OB.
| 2 |
| 2 |
解答: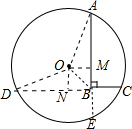 解:延长AB、CB分别交⊙O于E、D,作OM⊥AB于M,ON⊥CD于N,连结OB、OA、OD,如图,设OM=a,ON=b,
解:延长AB、CB分别交⊙O于E、D,作OM⊥AB于M,ON⊥CD于N,连结OB、OA、OD,如图,设OM=a,ON=b,
∵∠ABC=90°
∴四边形OMBN为矩形,
∴OM=BN=a,ON=BM=b,
∵ON⊥CD,
∴DN=CN=BN+BC=a+2,
在△AOM中,∵AM=AB-BM=6-b,OM=a,OA=5
,
∴(6-b)2+a2=(5
)2①,
在Rt△OND中,∵ON2+DN2=OD2,
∴(a+2)2+b2=(5
)2②,
由①-②得a=8-3b③,
把③代入①得(6-b)2+(8-3b)2=(5
)2,
整理得b2-6b+5=0,解得b1=5,b2=1,
当b=5时,a=-7(舍去);当b=1时,a=5,
在Rt△OBM中,∵BM=1,OM=5,
∴OB=
=
,
即点B到圆心的距离为
.
 解:延长AB、CB分别交⊙O于E、D,作OM⊥AB于M,ON⊥CD于N,连结OB、OA、OD,如图,设OM=a,ON=b,
解:延长AB、CB分别交⊙O于E、D,作OM⊥AB于M,ON⊥CD于N,连结OB、OA、OD,如图,设OM=a,ON=b,∵∠ABC=90°
∴四边形OMBN为矩形,
∴OM=BN=a,ON=BM=b,
∵ON⊥CD,
∴DN=CN=BN+BC=a+2,
在△AOM中,∵AM=AB-BM=6-b,OM=a,OA=5
| 2 |
∴(6-b)2+a2=(5
| 2 |
在Rt△OND中,∵ON2+DN2=OD2,
∴(a+2)2+b2=(5
| 2 |
由①-②得a=8-3b③,
把③代入①得(6-b)2+(8-3b)2=(5
| 2 |
整理得b2-6b+5=0,解得b1=5,b2=1,
当b=5时,a=-7(舍去);当b=1时,a=5,
在Rt△OBM中,∵BM=1,OM=5,
∴OB=
| OM2+BM2 |
| 26 |
即点B到圆心的距离为
| 26 |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
相关题目