Question

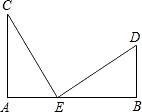已知，如图，AC⊥AB，DB⊥AB，AC=BE，AE=BD，
（1）求证：△CAE≌△EBD；
（2）连接CD，试判断△CDE的形状．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）易证∠CAE=∠EBD=90°，即可证明△CAE≌△EBD，即可解题；
（2）根据（1）中结论可得∠CEA=∠BDE，CE=DE，根据∠BDE+∠BED=90°可以求得∠CED=90°，即可判定△CDE为等腰直角三角形，即可解题．

解答：证明：（1）∵AC⊥AB，DB⊥AB，
∴∠CAE=∠EBD=90°，
在△CAE和△EBD中，

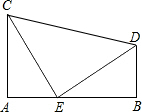
AC=BE ∠CAE=∠EBD=90° AE=BD

，
∴△CAE≌△EBD（SAS）；
（2）作出图形，

∵△CAE≌△EBD，
∴∠CEA=∠BDE，CE=DE，
∵∠BDE+∠BED=90°，
∴CEA+∠BED=90°，
∴∠CED=90°，
∴△CDE为等腰直角三角形．

点评：本题考查了全等三角形的判定，考查了全等三角形对应边、对应角相等的性质，本题中求证△CAE≌△EBD是解题的关键．