题目内容
3. 如图,在△ABC中,点D是边BC中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点P在边AB上,EF∥BC.
如图,在△ABC中,点D是边BC中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点P在边AB上,EF∥BC.(1)求证:四边形BDEF是平行四边形.
(2)线段BF,AB,AC存在什么数量关系?证明你得到的结论.
分析 (1)要证明四边形BDEF是平行四边形,根据题意可以得到判定四边形BDEF是平行四边形的条件,EF和BD,DE和BF的关系,本题得以解决;
(2)首先写出线段BF,AB,AC存在的数量关系,然后根据题目中的条件进行证明即可.
解答 (1)证明;∵AE平分∠BAC,CE⊥AE,
∴△APC是等腰三角形,
∴AP=AC,点E是PC的中点,
又∵点D是BC的中点,
∴DE∥BF,
又∵EF∥BC,
∴四边形BDEF是平行四边形;
(2)线段BF,AB,AC之间的数量关系是:AB=2BF+AC,
证明:∵AE平分∠BAC,CE⊥AE,
∴△APC是等腰三角形,
∴AP=AC,
由(1)知BF=DE,
∵点E是PC的中点,点D是BC的中点,
∴DE=$\frac{1}{2}$BP,
∴BF=$\frac{1}{2}$BP,
∵AB=BP+AP,
∴AB=2BF+AC.
点评 本题考查平行四边形的判定与性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
 如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )| A. | 2:3 | B. | 3:4 | C. | 1:1 | D. | 4:3 |
12. 如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
 如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )
如图,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=( )| A. | 63°30′ | B. | 53°30′ | C. | 73°30′ | D. | 93°30′ |
13.若2m2-3m-7=0,7n2+3n-2=0,其中m,n为实数,且mn≠1,则m+$\frac{1}{n}$=( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{2}$ | D. | $-\frac{7}{2}$ |
 与
与 的大小有什么关系?为什么?
的大小有什么关系?为什么?
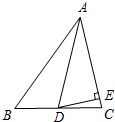 如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°.
如图,在△ABC中,AD是角平分线,∠B=45°,∠C=76°.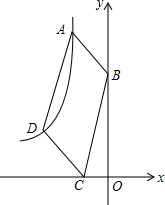 如图,在平面直角坐标系xOy中,已知A(1-$\sqrt{5}$,1+$\sqrt{5}$),B(0,1),双曲线y=$\frac{k}{x}$经过?ABCD的顶点A、D,求D点的坐标.
如图,在平面直角坐标系xOy中,已知A(1-$\sqrt{5}$,1+$\sqrt{5}$),B(0,1),双曲线y=$\frac{k}{x}$经过?ABCD的顶点A、D,求D点的坐标.