题目内容
解方程：
（1）7x（5x+2）=6（5x+2）；
（2）2x2-12x=36（配方法）
（1）7x（5x+2）=6（5x+2）；
（2）2x2-12x=36（配方法）
考点：解一元二次方程-因式分解法,解一元二次方程-配方法
专题：计算题
分析：（1）先移项得到7x（5x+2）-6（5x+2）=0，然后利用因式分解法解方程；
（2）先变形为x2-6x=18，然后利用配方法解方程．
（2）先变形为x2-6x=18，然后利用配方法解方程．
解答：解：（1）7x（5x+2）-6（5x+2）=0，
（5x+2）（7x-6）=0，
所以x1=-
，x2=
；
（2）x2-6x=18，
x2-6x+9=27，
（x-3）2=27，
x-3=±3
，
所以x1=3+3
，x2=3-3
．
（5x+2）（7x-6）=0，
所以x1=-
| 2 |
| 5 |
| 6 |
| 7 |
（2）x2-6x=18，
x2-6x+9=27，
（x-3）2=27，
x-3=±3
| 3 |
所以x1=3+3
| 3 |
| 3 |
点评：本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
练习册系列答案
相关题目
已知二次函数y=ax2+bx+c（a≠0）的图象经过点A（1，0），B（0，-3），且对称轴为x=2，则这条抛物线的顶点坐标为（ ）
| A、（2，3） |
| B、（2，1） |
| C、（-2，1） |
| D、（2，-1） |
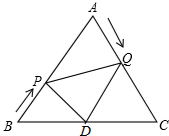已知△ABC是边长为6cm的等边三角形，动点P、Q同时从B、A两点出发，分别沿BA、AC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：
如图是由8个相同的小立方块搭成的几何体，已知它的左视图如下，请画出它的主视图和俯视图．如果一组数据3，7，2，a，4，6的平均数是5，则a的值是（ ）
| A、8 | B、5 | C、4 | D、3 |
如图，燃烧的蜡烛AB经小孔O在屏幕上成像A′B′．设AB=30cm，小孔O到AB，A′B′的距离分别为32cm、20cm，求像A′B′的长．