题目内容
 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=4
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图,已知EF=4| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:垂径定理的应用,勾股定理,扇形面积的计算
专题:
分析:连接OE,OF,过点O作OG⊥EF于点G,由垂径定理求出EG的长,设OE=r,在Rt△OEG中根据勾股定理可求出r的值,进而得出∠EOG的度数,由S阴影=S扇形-S△EOF即可得出结论.
解答: 解:连接OE,OF,过点O作OG⊥EF于点G,
解:连接OE,OF,过点O作OG⊥EF于点G,
∵EF=4
cm,
∴EG=
EF=2
cm,
设OE=r,则OG=CD-r=6-r,
在Rt△OEG中,
∵EG=2
cm,OE=r,OG=6-r,OG2+EG2=OE2,
∴(6-r)2+(2
)2=r2,
解得r=4,
∴OG=2cm,
∵OG=
OE,
∴∠OEG=30°,
∴∠EOG=60°,
∴∠EOF=2∠EOG=120°,
∴S阴影=S扇形EOF-S△EOF=
-
×4
×2=(
π-4
)cm2.
故选C.
 解:连接OE,OF,过点O作OG⊥EF于点G,
解:连接OE,OF,过点O作OG⊥EF于点G,∵EF=4
| 3 |
∴EG=
| 1 |
| 2 |
| 3 |
设OE=r,则OG=CD-r=6-r,
在Rt△OEG中,
∵EG=2
| 3 |
∴(6-r)2+(2
| 3 |
解得r=4,
∴OG=2cm,
∵OG=
| 1 |
| 2 |
∴∠OEG=30°,
∴∠EOG=60°,
∴∠EOF=2∠EOG=120°,
∴S阴影=S扇形EOF-S△EOF=
| 120π×42 |
| 360 |
| 1 |
| 2 |
| 3 |
| 16 |
| 3 |
| 3 |
故选C.
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图,AO⊥OB,垂足为O,OC平分∠AOB,则∠AOC的度数为( )
如图,AO⊥OB,垂足为O,OC平分∠AOB,则∠AOC的度数为( )| A、30° | B、40° |
| C、45° | D、90° |
 在正方形的网格中,⊙O经过小正方形的顶点A、B、C、D,P是⊙O上的一点,则圆周角∠P的正切值为( )
在正方形的网格中,⊙O经过小正方形的顶点A、B、C、D,P是⊙O上的一点,则圆周角∠P的正切值为( )A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
 如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的最多个数是( )
如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的最多个数是( )| A、9个 | B、8个 | C、7个 | D、6 |
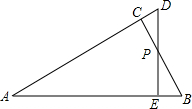 把两个一样的直角三角板的30°角重合,其两对边交于点P(如图),连接BD,下列说法错误的是( )
把两个一样的直角三角板的30°角重合,其两对边交于点P(如图),连接BD,下列说法错误的是( )| A、整个图形是轴对称图形 |
| B、△PEB周长大于DB |
| C、有4对全等三角形(不添线) |
| D、∠EDB=15° |
 如图,已知函数y=3x+1和y=ax-3的图象交于点P(m,-5),则根据图象可得不等式3x+1<ax-3的解集是
如图,已知函数y=3x+1和y=ax-3的图象交于点P(m,-5),则根据图象可得不等式3x+1<ax-3的解集是 将一副三角尺如图放置,则∠APD=
将一副三角尺如图放置,则∠APD=