题目内容
1.计算$\frac{2m}{{m}^{2}-9}$+$\frac{1}{3-m}$的结果是( )| A. | $\frac{1}{m-3}$ | B. | $\frac{1}{m+3}$ | C. | $\frac{3}{m-3}$ | D. | $\frac{6}{3-m}$ |
分析 原式通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=$\frac{2m}{(m+3)(m-3)}$-$\frac{m+3}{(m+3)(m-3)}$=$\frac{m-3}{(m+3)(m-3)}$=$\frac{1}{m+3}$,
故选B
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
12.-(+2)的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
16.下列计算结果正确的是( )
| A. | -3.5÷$\frac{7}{8}$×($-\frac{3}{4}$)=-3 | B. | -2÷3×3=-$\frac{2}{9}$ | C. | (-6)÷(-4)÷(+$\frac{6}{5}$)=$\frac{5}{4}$ | D. | -$\frac{1}{30}$÷($\frac{1}{6}$÷$\frac{1}{5}$)=-1 |
13. 如图,在△ABC中,AB=AC,∠A=70°,∠OBC=∠OCA,则∠BOC的度数为( )
如图,在△ABC中,AB=AC,∠A=70°,∠OBC=∠OCA,则∠BOC的度数为( )
 如图,在△ABC中,AB=AC,∠A=70°,∠OBC=∠OCA,则∠BOC的度数为( )
如图,在△ABC中,AB=AC,∠A=70°,∠OBC=∠OCA,则∠BOC的度数为( )| A. | 140° | B. | 110° | C. | 125° | D. | 115° |
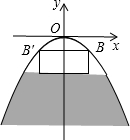 某河上由抛物线形拱桥,当水面距拱顶5m时,水面宽8m,一木船宽4m,高2m,载货后,木船露出水面的部分为$\frac{3}{4}$m,问:水面涨到与抛物线拱顶相距多少米时,木船开始不能通航?
某河上由抛物线形拱桥,当水面距拱顶5m时,水面宽8m,一木船宽4m,高2m,载货后,木船露出水面的部分为$\frac{3}{4}$m,问:水面涨到与抛物线拱顶相距多少米时,木船开始不能通航?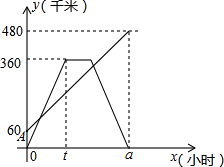 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题: 如图,I是△ABC的内心,∠BAC的平分线和△ABC的外接圆相交于点D.BD与ID相等吗?为什么?
如图,I是△ABC的内心,∠BAC的平分线和△ABC的外接圆相交于点D.BD与ID相等吗?为什么?