题目内容
6.已知二次函数y=$\frac{1}{3}$(x+2)2-$\frac{3}{4}$,则当x=-2时,函数有最小值是-$\frac{3}{4}$.分析 根据抛物线的顶点坐标和抛物线的开口方向可以得到答案.
解答 解:∵y=$\frac{1}{3}$(x+2)2-$\frac{3}{4}$,
∴该抛物线的顶点坐标是(-2,-$\frac{3}{4}$),且抛物线开口方向向上,
∴当x=-2时,y取得最小值-$\frac{3}{4}$.
故答案是:-2,小,-$\frac{3}{4}$.
点评 本题考查了二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图所示,根据有理数a,b,c在数轴上的位置,比较a,b,c的大小关系是( )
如图所示,根据有理数a,b,c在数轴上的位置,比较a,b,c的大小关系是( )
 如图所示,根据有理数a,b,c在数轴上的位置,比较a,b,c的大小关系是( )
如图所示,根据有理数a,b,c在数轴上的位置,比较a,b,c的大小关系是( )| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
1.计算$\frac{2m}{{m}^{2}-9}$+$\frac{1}{3-m}$的结果是( )
| A. | $\frac{1}{m-3}$ | B. | $\frac{1}{m+3}$ | C. | $\frac{3}{m-3}$ | D. | $\frac{6}{3-m}$ |
18.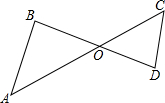 如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
 如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )
如图,线段AC,BD交于点O,由下列条件,不能得出△AOB∽△DOC的是( )| A. | $\frac{OB}{OC}$=$\frac{OA}{OD}$ | B. | $\frac{OA}{OB}$=$\frac{OD}{OC}$ | C. | $\frac{OA}{OD}$=$\frac{AB}{CD}$ | D. | $\frac{OC}{OB}$=$\frac{OD}{OA}$ |
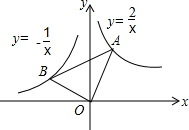 如图,在x轴的上方,∠BOA(直角)绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则△AOB面积的最小值为$\sqrt{2}$.
如图,在x轴的上方,∠BOA(直角)绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点,则△AOB面积的最小值为$\sqrt{2}$.
 如图,在正方形ABCD中,E为AB的中点,当$\frac{AF}{AD}$=$\frac{1}{3}$时,△AEF∽△BCE.
如图,在正方形ABCD中,E为AB的中点,当$\frac{AF}{AD}$=$\frac{1}{3}$时,△AEF∽△BCE.